Fisica classica/Campi elettromagnetici nei dielettrici

Se si riscrivono le equazioni di Maxwell in presenza di materia, immaginando che non vi siano né cariche libere né correnti di conduzione, si arriva anche nei dielettrici, cioè i materiali isolanti, ad una equazione delle onde:

${\mathrm{\nabla }}^2\overrightarrow{E}=\frac{1}{c{\text{'}}^2}\frac{{\partial }^2\overrightarrow{E}}{\partial t^2}$

La differenza è che la velocità della luce ha un valore inferiore a quello del vuoto:

$c^{\prime }=\frac{c}{n}$

Infatti $n$ chiamato indice di rifrazione è sempre maggiore di 1. Finché le onde elettromagnetiche hanno frequenze basse ( minori di qualche centinaio di MHz) $n$ è semplicemente

$n=\sqrt{{ϵ}_r{\mu }_r}$

Dove ${ϵ}_r$ è la costante dielettrica relativa (sempre maggiore di 1) e ${\mu }_r$ è la permeabilità magnetica relativa, che nella maggior parte delle sostanze è prossima all'unità. Quindi se consideriamo, ad esempio, l'acqua, deionizzata cioè senza elettroliti in soluzione, la quale ha una costante dielettrica relativa pari a 80, la velocità della luce per quanto riguarda le basse frequenze è circa 1/9 di quella nel vuoto.

Lunghezza d'onda

Se definiamo ${\lambda }_o$ la lunghezza d'onda nel vuoto. Immaginiamo di avere una onda elettromagnetica che dal vuoto, in cui vale:

${\lambda }_o\nu =c$

passa ad un mezzo dielettrico, la relazione che lega lunghezza d'onda e frequenza propria di tutte le onde vale anche in presenza di dielettrico continua a valere: La relazione che lega lunghezza d'onda e frequenza propria di tutte le onde vale anche in presenza di dielettrico essendo:

$\lambda \nu =c^{\prime }=\frac{c}{n}$

La relazione che lega lunghezza d'onda e frequenza propria di tutte le onde vale anche in presenza di dielettrico essendo:

$\lambda =\frac{{\lambda }_o}{n}$

quindi in genere nei mezzi la lunghezza d'onda diminuisce

Dispersione

A frequenze superiori a un centinaio di MHz, se si tiene in considerazione la spiegazione microscopica della costante dielettrica relativa, bisogna introdurre la polarizzazione del dielettrico. La Polarizzazione non risponde istantaneamente se il campo elettrico presente localmente oscilla ad una frequenza elevata,. Inoltre vi è un assorbimento delle onde elettromagnetiche da parte del dielettrico. Per tenere in conto di entrambi gli aspetti, la riduzione della velocità della luce e lo sfasamento della polarizzazione, si introduce un indice di rifrazione complesso (indicato con un tilde) :

$\tilde{n}=n-j\kappa$

Dove la parte reale determina la velocità (di fase) dell'onda alla frequenza considerata, mentre κ chiamato coefficiente di estinzione, da un'idea di quanta parte dell'onda viene assorbita nell'attraversamento del mezzo. Sia n che κ dipendono dalla frequenza.

La variazione di n con la frequenza va sotto il nome di dispersione, fenomeno molto evidente in ottica, ma presente in un vasto intervallo di frequenze.

Spiegazione microscopica della dispersione

L'equazione microscopica che descrive l'azione del campo elettrico sui dipoli elementari di cui è fatta la materia è simile a quella di un oscillatore armonico forzato con un termine di smorzamento. Tale sistema ammette una frequenza di risonanza, al crescere della frequenza, fino a quando il materiale ha un assorbimento κ, n tende a crescere. In corrispondenza della frequenza di risonanza dove κ è massimo n può diventare inferiore all'unità. In pratica si ha che ad esempio l'acqua alle frequenze ottiche ha un indice di rifrazione di appena 1.33 (invece di 9 come ci si aspetterebbe dal fatto che $n=\sqrt{{\epsilon }_r}$ essendo nell'acqua ${\epsilon }_r=80$).

Un semplice modello a livello atomico rende conto di cosa avviene.

Prima osserviamo il fenomeno dal punto di vista dell'elettrostatica, cioè Consideriamo un atomo di numero atomico $Z$, immaginato come una sfera. In assenza di campo elettrico il centro delle cariche positive: nucleo coincide con il centro delle cariche negative (la distribuzione degli elettroni). Se applichiamo un campo elettrico esterno $\overrightarrow{E}$ avrò che l'atomo si deformerà (molto debolmente) in quanto il campo elettrico esercita una azione eguale ed opposta sul nucleo e sugli elettroni: la deformazione $\overrightarrow{\delta }$ sarà proporzionale al campo elettrico applicato con una costante di proporzionalità $\alpha$ dipendente dall'atomo considerato, in maniera tale che:

$\alpha \overrightarrow{\delta }=Ze\overrightarrow{E}$

Dove $e$ è la carica elementare. Conoscendo la massa dell'atomo possiamo definire con

${\omega }_o^2=\frac{\alpha }{m}$

Cosicché la deformazione vale:

$\overrightarrow{\delta }=\frac{Ze}{m{\omega }_o^2}\overrightarrow{E}$

Quindi si ha che viene indotto un momento di dipolo pari a:

$\overrightarrow{p}=Ze\overrightarrow{\delta }=\frac{(Ze{)}^2}{m{\omega }_o^2}\overrightarrow{E}$

Se quindi la densità di atomi per unità di volume vale $N$ (non si usa il simbolo n per non fare confusione con l'indice di rifrazione):

$\overrightarrow{P}=N\frac{(Ze{)}^2}{m{\omega }_o^2}\overrightarrow{E}$

Essendo anche:

$\overrightarrow{P}={ϵ}_o({ϵ}_r-1)\overrightarrow{E}$

si ha che:

${ϵ}_r=1+N\frac{(Ze{)}^2}{{ϵ}_{o}m{\omega }_o^2}$

Tanto maggiormente gli atomi sono deformabili tanto maggiore sarà la costante dielettrica relativa, così al tendere di $N$ a zero la costante dielettrica relativa tende ad 1.

Nella dinamica consideriamo un campo elettrico è variabile nel tempo che localmente ha una espressione del tipo:

$E=E_o{e}^{j\omega t}$

Notare come per semplicità si sia considerato un caso unidimensionale, per cui si è omesso il simbolo di vettore. L'equazione della dinamica è:

$m\ddot{\delta }+m\gamma \dot{\delta }+m{\omega }_o^2\delta =Ze{E}_o{e}^{j\omega t}$

Tiene conto sia del termine di richiamo elastico ($m{\omega }_o^2\delta$ considerato prima), ma viene aggiunto un termine di dissipazione viscosa ($m\gamma \dot{\delta }$ ) con $\gamma$ che tiene conto delle perdite nel dielettrico.

L'equazione è formalmente eguale a quella di un oscillatore armonico forzato con un termine di smorzamento Se la soluzione per $\delta$ è del tipo:

$\delta ={\delta }_o{e}^{j\omega t}$

che sostituita nell'equazione della dinamica si traduce in una equazione per ${\delta }_o$:

$-m{\omega }^2{\delta }_o+j\omega m\gamma {\delta }_o+m{\omega }_o^2{\delta }_o=Ze{E}_o$

da cui:

${\delta }_o=\frac{Ze{E}_o}{m({\omega }_o^2-{\omega }^2+j\omega \gamma )}$

Ripetendo il ragionamento precedente, mutatis mutandis, si ha che:

$\overrightarrow{P}=N\frac{(Ze{)}^2}{m({\omega }_o^2-{\omega }^2+j\omega \gamma )}\overrightarrow{E}$

quindi la costante dielettrica relativa è complessa e la sua espressione è:

${ϵ}_r=1+N\frac{(Ze{)}^2}{{ϵ}_{o}m({\omega }_o^2-{\omega }^2+j\omega \gamma )}$

Di conseguenza anche l'indice di rifrazione è complesso e vale:

$\tilde{n}=\frac{1}{\sqrt{{ϵ}_r}}=n-j\kappa$

Con

$n=1+\frac{N(Ze{)}^2({\omega }_o^2-{\omega }^2)}{{ϵ}_{o}m[({\omega }_o^2-{\omega }^2{)}^2+{\omega }^2{\gamma }^2)]}$

$\kappa =\frac{N(Ze{)}^2\gamma \omega }{2{ϵ}_{o}m[({\omega }_o^2-{\omega }^2{)}^2+{\omega }^2{\gamma }^2)]}$

Il loro comportamento è mostrato nelle figure a fianco. Quindi in corrispondenza della frequenza di risonanza si ha che la velocità della luce diminuisce, ma contemporaneamente aumenta vistosamente l'assorbimento.

La rappresentazione esponenziale rende meglio conto del significato di $n$ e $\kappa$. Nella rappresentazione esponenziale possiamo scrivere una onda piana monodimensionale propagantesi sull'asse delle $x$

$\overrightarrow{E}={\overrightarrow{E}}_o{e}^{j\omega (t-x/v)}$

Ora se al posto di v sostituiamo $c/\tilde{n}$

$\overrightarrow{E}={\overrightarrow{E}}_o{e}^{j\omega [t-(n-j\kappa )x/c]}={\overrightarrow{E}}_o{e}^{-\omega \kappa x/c}{e}^{j\omega (t-nx/c)}$

La trasmissione delle onde elettromagnetiche nell'atmosfera a lunghezze d'onda nel vicino infrarosso

Il termine $\omega \kappa /c$ detto coefficiente di assorbimento ha le dimensioni di una lunghezza alla -1. Tanto maggiore è il suo valore più rapidamente si estingue l'ampiezza dell'onda attraversando il mezzo.

La figura mostra l'opacità dell'atmosfera nel vicino infrarosso (lunghezze d'onda tra 14 microns e 700 nm). L'opacità è una misura del coefficiente di assorbimento. Alcune molecole presenti nell'atmosfera hanno caratteristiche frequenze di risonanza indicate sull'asse delle ascisse.

Velocità di fase e velocità di gruppo

Per ragioni di semplicità si considera il caso unidimensionale di onde piane.

Si definisce velocità di fase:

$v_f=\frac{\omega }{k}$

Mentre si definisce velocità di gruppo:

$v_g=\frac{\partial \omega }{\partial k}$

Consideriamo la propagazione in un mezzo di un pacchetto d'onda cioè una sovrapposizione di onde piane:

$E(x,t)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}dkA(k)e^{i(kx-\omega t)},$

La funzione $A(k),$ è il peso delle varie onde piane sovrapposte.

linea piena: un pacchetto d'onda. Linea tratteggiata: l'inviluppo di un pacchetto d'onda fotografato ad un certo istante di tempo. L'inviluppo si muove con la velocità di gruppo .

Viene mostrata un pacchetto d'onda con la velocità di fase che va in direzione opposta a quella di gruppo. La velocità di gruppo, l'inviluppo si muove verso destra, mentre la velocità di fase è negativa (i picchi e gli avvallamenti) si muovono verso sinistra

.

La velocità di gruppo di un'onda è la velocità con cui l'inviluppo totale dell'onda si propaga nello spazio.

La funzione $\omega (k)$, tra la pulsazione ed il numero d'onda, è conosciuta come relazione di dispersione.

Se il mezzo non è dispersivo si ha che la relazione di dispersione è semplicemente:

$\omega =c^{\prime }k,$

in questo caso, la velocità di gruppo coincide con quella di fase, ed una onda di qualsiasi forma si muoverà non distorta a questa velocità.

Se invece la relazione di dispersione è diversa anche semplicemente:

$\omega =c^{\prime }k+cost,$

Le due velocità non coincidono: in questo caso l'inviluppo si muoverò con la velocità di gruppo, mentre i picchi e le valli si muoveranno con la velocità di fase.

Se il pacchetto d'onda è costituito da un piccolo intervallo di frequenze, possiamo considerare $\omega (k),$ approssimativamente lineare in questo intervallo. Consideriamo cioè un pacchetto d'onda, quasi monocromatico, centrato attorno alla pulsazione attorno a ${\omega }_o,$, con una relazione di dispersione:

$\omega (k)\approx {\omega }_0+(k-k_0)(d\omega /dk{)}_{\omega }={\omega }_0+(k-k_0)v_g$

Sostituendo, la relazione di dispersione, nella espressione generale del pacchetto d'onda, dopo semplici passaggi algebrici:

$E(x,t)=e^{i(k_{0}x-{\omega }_{0}t)}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}dkA(k)e^{i(k-k_0)(x-v_{g}t)}.$

Ci sono due termini in questa espressione:

Il primo termine, $e^{i(k_{0}x-{\omega }_{0}t)}$, descrive un'onda monocromatica, con numero d'onda $k_0$, con picchi e avvallamenti che si muovono alla velocità di fase all'interno dell'inviluppo del pacchetto d'onda.

L'altro termine è l'inviluppo del pacchetto d'onda:

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}dkA(k)e^{i(k-k_0)(x-v_{g}t)}$,

Questa funzione inviluppo dipende dalla posizione e dal tempo solo attraverso la combinazione di $(x-\omega {\text{'}}_{0}t)$.

Perciò, l'inviluppo di un pacchetto d'onda viaggia alla velocità di gruppo.

Passaggio da un mezzo ad un altro

Un'onda elettromagnetica che colpisce l'interfaccia tra due mezzi di divide in due: una parte viene riflessa e una parte viene rifratta.

Quando una onda piana monocromatica va da un mezzo con un dato indice di rifrazione n₁ verso un secondo mezzo con indice n₂, possono verificarsi sia la riflessione che la rifrazione dell'onda luminosa stessa.

Nella figura a destra, un'onda elettromagnetica incidente PO colpisce al punto O l'interfaccia tra due mezzi con indici di rifrazione n₁ e n₂. Parte del raggio viene riflessa come raggio OQ e parte viene rifratta seguendo la traiettoria OS. Gli angoli che l'onda incidente, riflessa e rifratta formano con la normale all'interfaccia sono θ_i, θ_r e θ_t, rispettivamente.

Le proprietà sono state studiate già nella metà del XVII secolo da Fermat a partire da un semplice principio:

Fra tutti i cammini possibili la luce sceglie sempre il cammino (detto cammino ottico) che richiede il più breve tempo per essere percorso.

Tali proprietà in realtà sono state formulate per la parte dello spettro che si conosceva allora: l'ottica; ma in realtà tale principio vale per tutte le onde elettromagnetiche piane.

Riflessione

Legge di Fermat applicata alla riflessione da una superficie, gli angoli ${\theta }_1$ e ${\theta }_2$ sono quelli che nella figura precedente e nel testo sono chiamati ${\theta }_i$ (raggio incidente) e ${\theta }_r$ (raggio riflesso)

Usiamo il teorema di Fermat per derivare le leggi della riflessione. Immaginiamo di volere andare da un punto A ad un punto B, disposti come in figura cioè riflettendo sulla superficie piana S. Indichiamo con $(x_A,y_A,0)$, $(x_B,y_B,0)$ le coordinate dei punti A e B. Scegliamo il piano x,y passante per i punti A e B (per questo la terza coordinata è nulla). Scegliamo inoltre l'asse delle y passante per il punto di incidenza (x,0,z) da determinare. Il tempo impiegato dalla luce nel mezzo in cui si propaga con velocità c' sarà:

$t=\frac{\sqrt{(x-x_A{)}^2+y_A^2+z^2}}{c^{\prime }}+\frac{\sqrt{(x-x_B{)}^2+y_B^2+z^2}}{c^{\prime }}$

Se deriviamo la derivata rispetto a z di tale equazione e la poniamo eguale a zero (troviamo lo z per cui la funzione ha un minimo, che sia un minimo davvero lo rivela la derivata seconda). Il valore della derivata prima posta eguale a 0:

$z(\frac{1}{\sqrt{(x-x_A{)}^2+y_A^2+z^2}}+\frac{1}{\sqrt{(x-x_B{)}^2+y_B^2+z^2}})=0$

Essendo il termine dentro parentesi sempre maggiore di 0, la somma degli inversi di due distanze, occorre che z=0. Quindi i raggi incidente e riflesso sono contenuti nel piano individuato dal raggio incidente e dalla normale alla superficie passante per il punto di incidenza. Quindi l'equazione sul tempo totale diviene:

$t=\frac{\sqrt{(x-x_A{)}^2+y_A^2}}{c^{\prime }}+\frac{\sqrt{(x-x_B{)}^2+y_B^2}}{c^{\prime }}$

Derivando nella sola variabile x rimasta e annullandola si ha che:

$\frac{x-x_A}{\sqrt{(x-x_A{)}^2+y_A^2}}+\frac{x-x_B}{\sqrt{(x-x_B{)}^2+y_B^2}}=0$

Dalla costruzione geometrica il primo termine è il seno dell'angolo ${\theta }_1$, l'angolo che forma il raggio incidente con la normale al piano passante per il punto di incidenza. Mentre il secondo termine è il seno cambiato di segno,dell'angolo che il raggio riflesso forma con la normale al piano:

$\sin {\theta }_i=\sin {\theta }_r$

e quindi:

${\theta }_i={\theta }_r$

La legge della riflessione: L'angolo di incidenza e di riflessione sono eguali.

L'ipotesi di superficie piana significa che la rugosità della interfaccia sia trascurabile rispetto alla lunghezza d'onda. Quindi per onde millimetriche una rugosità di frazione di millimetri rappresenta una superficie piana. Mentre per la luce, che ha lunghezze d'onda di frazioni di la condizione di superficie piana corrisponde ad un

Rifrazione

Legge di Fermat applicata alla rifrazione tra due mezzi. Gli angoli ${\theta }_1$ e ${\theta }_2$ sono quelli che nella prima figura e nel testo identificati con ${\theta }_i$ (raggio incidente) e ${\theta }_t$ (raggio trasmesso)

Usiamo il teorema di Fermat per derivare le leggi della rifrazione.

Quando un raggio di luce attraversa la superficie di separazione tra due mezzi diversi trasparenti con velocità della luce c₁ e c₂. Cioè studiamo la rifrazione come mostrato nella figura a fianco. Come per le leggi della riflessione, supponiamo che la separazione tra i due mezzi sia piana.

Indichiamo con $(x_A,y_A,0)$, $(x_B,y_B,0)$ le coordinate dei punti A e B. Scegliamo il piano x,y passante per i punti A e B (per questo la terza coordinata è nulla). Scegliamo inoltre l'asse delle y passante per il punto di incidenza (x,0,z) da determinare. Il tempo totale impiegato dal raggio per andare dal punto A e B sarà:

$t=\frac{\sqrt{(x-x_A{)}^2+y_A^2+z^2}}{c_1}+\frac{\sqrt{(x-x_B{)}^2+y_B^2+z^2}}{c_2}$

Se deriviamo la derivata rispetto a z di tale equazione e la poniamo eguale a zero (troviamo lo z per cui la funzione ha un minimo, che sia un minimo davvero lo rivela la derivata seconda). Il valore della derivata prima posta eguale a 0:

$z(\frac{1}{c_1\sqrt{(x-x_A{)}^2+y_A^2+z^2}}+\frac{1}{c_2\sqrt{(x-x_B{)}^2+y_B^2+z^2}})=0$

Essendo il termine dentro parentesi sempre maggiore di 0, la somma degli inversi di due distanze, occorre che z=0. Quindi i raggi incidente e rifratto sono contenuti nel piano individuato dal raggio incidente e dalla normale alla superficie passante per il punto di incidenza. Quindi l'equazione sul tempo totale si riduce a:

$t=\frac{\sqrt{(x-x_A{)}^2+y_A^2}}{c_1}+\frac{\sqrt{(x-x_B{)}^2+y_B^2}}{c_2}$

Derivando nella sola variabile x rimasta e annullandola si ha che:

$\frac{x-x_A}{c_1\sqrt{(x-x_A{)}^2+y_A^2}}+\frac{x-x_B}{c_2\sqrt{(x-x_B{)}^2+y_B^2}}=0$

da cui:

$\frac{\sin {\theta }_i}{c_1}=\frac{\sin {\theta }_t}{c_2}$

ossia:

$\frac{\sin {\theta }_i}{\sin {\theta }_t}=\frac{c_1}{c_2}=\frac{n_2}{n_1}$

La legge della rifrazione: Il rapporto tra il seno dell'angolo di incidenza ed il seno dell'angolo di rifrazione è costante ed eguale al rapporto della velocità della luce nei due mezzi. Spesso scritta come:

$n_1\sin {\theta }_i=n_2\sin {\theta }_r$

Notiamo che se $n_1>n_2$, l'angolo di rifrazione sarà maggiore dell'angolo di incidenza; esisterà dunque un angolo ${\theta }_i$ tale che ${\theta }_r=90^0$ quindi:

$\sin {\theta }_{limite}=\frac{n_2}{n_1}$

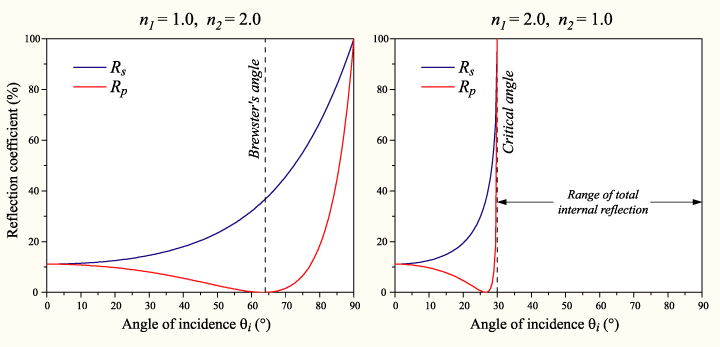
Tale angolo è detto angolo limite (o critico). Infatti, per un angolo di incidenza superiore a tale valore non vi è nessun raggio diffratto. Tale fenomeno, su ci si basa la propagazione delle onde elettromagnetiche nelle fibre ottiche, è chiamato riflessione totale.

Anche la spiegazione fisica del miraggio è basata su tale fenomeno. Esso si verifica quando i raggi del Sole incontrano uno strato d'aria più calda rispetto agli strati sovrastanti dove l'aria più fredda e di densità maggiore. Così i raggi di luce subiscono una riflessione totale ed è possibile vedere le immagini come se fossero veramente riflesse al suolo.

Leggi di Fresnel

Grazie alle leggi di Fresnel è possibile calcolare come l'intensità di un'onda elettromagnetica incidente su una superficie viene ripartita tra il raggio riflesso e il raggio rifratto.

Per ricavare tali leggi si descrive l'onda incidente come:

${\overrightarrow{E}}_i={\overrightarrow{E}}_{io}{e}^{j({\overrightarrow{k}}_i\cdot \overrightarrow{r}-\omega t)}$

indicando con ${\overrightarrow{k}}_i$ il vettore d'onda incidente.

L'onda riflessa, nello stesso punto spazio del raggio riflesso:

${\overrightarrow{E}}_r={\overrightarrow{E}}_{ro}{e}^{j({\overrightarrow{k}}_r\cdot \overrightarrow{r}-\omega t)}$

indicando con ${\overrightarrow{k}}_r$ il vettore d'onda riflesso. Tale vettore in modulo è eguale a ${\overrightarrow{k}}_i$.

L'onda trasmessa, sempre nello stesso punto:

${\overrightarrow{E}}_t={\overrightarrow{E}}_{to}{e}^{j({\overrightarrow{k}}_t\cdot \overrightarrow{r}-\omega t)}$

indicando con ${\overrightarrow{k}}_r$ il vettore d'onda riflesso, notiamo $|k_r|/|k_i|=n_1/n_2$

Ai vettori ${\overrightarrow{E}}_i,{\overrightarrow{E}}_r,{\overrightarrow{E}}_t$ sono associati i campi magnetici normali:

${\overrightarrow{B}}_i=\frac{n_1}{c}{\hat{k}}_i\times {\overrightarrow{E}}_i{\overrightarrow{B}}_r=\frac{n_1}{c}{\hat{k}}_r\times {\overrightarrow{E}}_r{\overrightarrow{B}}_t=\frac{n_2}{c}{\hat{k}}_t\times {\overrightarrow{E}}_t$

Tali onde sia che siano polarizzate o meno possono dividersi in componenti una con il campo elettrico perpendicolare al piano di incidenza (dato dalla direzione di propagazione dell'onda incidente e dalla normale all'interfaccia), detta polarizzazione S (senkrecht, perpendicolare in tedesco). L'altra nel piano di incidenza detta polarizzazione P (da parallela) .

Cioè posso scrivere:

${\overrightarrow{E}}_i=E_{iS}+E_{iP}{\overrightarrow{E}}_r=E_{rS}+E_{rP}{\overrightarrow{E}}_t=E_{tS}+E_{tP}$

${\overrightarrow{B}}_i=B_{iS}+B_{iP}{\overrightarrow{B}}_r=B_{rS}+B_{rP}{\overrightarrow{B}}_r=B_{rS}+B_{rP}$

Dalla condizione di raccordo nei dielettrici per quanto riguarda il campo elettrico la cui componente tangenziale è eguale nei due mezzi (la componente tangenziale alla superficie è quella chiamata ora P ):

$E_{S1}=E_{S2}⟶E_{iS}+E_{rS}=E_{tS}$

La componente normale del campo di induzione magnetica (B) nel passaggio da un mezzo all'altro è eguale, di conseguenza:

$B_{P1}=B_{P2}⟶n_1\cos {\theta }_i(E_{iS}+E_{rS})=n_2{E}_{tS}\cos {\theta }_t$

Analoghe condizioni di raccordo valgono per lo spostamento dielettrico (D) e il campo magnetico. Di conseguenza si hanno 4 equazioni, da cui con passaggi algebrici, la riflettanza per la componente perpendicolare (del campo elettrico):

$R_S={\left(\frac{E_{rS}}{E_{iS}}\right)}^2={\left[\frac{\sin ({\theta }_t-{\theta }_i)}{\sin ({\theta }_t+{\theta }_i)}\right]}^2$

mentre la riflettanza per la componente trasversa (quindi normale per il campo magnetico):

$R_P={\left(\frac{E_{rP}}{E_{iP}}\right)}^2={\left[\frac{\tan ({\theta }_t-{\theta }_i)}{\tan ({\theta }_t+{\theta }_i)}\right]}^2$

analogamente la trasmittanza perpendicolare:

$T_S=\frac{n_2}{n_1}{\left(\frac{E_{tS}}{E_{iS}}\right)}^2=\frac{n_2}{n_1}\frac{4{\sin }^2({\theta }_t){\cos }^2({\theta }_i)}{{\sin }^2({\theta }_t+{\theta }_i)}$

e la trasmittanza trasversa:

$T_P=\frac{n_2}{n_1}{\left(\frac{E_{tP}}{E_{iP}}\right)}^2=\frac{n_2}{n_1}\frac{4{\sin }^2({\theta }_t){\cos }^2({\theta }_i)}{{\sin }^2({\theta }_i+{\theta }_t){\cos }^2({\theta }_i-{\theta }_t)}$

Angolo di Brewster

Esiste un angolo particolare detto angolo di Brewster per il quale: $\tan ({\theta }_t+{\theta }_i)=\mathrm{\infty }$ e quindi $R_S=0$. Di conseguenza l'onda risulta polarizzata nella direzione perpendicolare al piano di incidenza cioè $R_P\ne 0$. L'angolo di Brewster è l'angolo di incidenza per cui:

${\theta }_B={\tan }^{-1}\frac{n_2}{n_1}$

infatti dovendo essere:

$\tan ({\theta }_t+{\theta }_i)=\mathrm{\infty }⟶{\theta }_t=\pi /2-{\theta }_i$

ma per la leggi di Snell:

$n_1\sin {\theta }_i=n_2\sin {\theta }_t$

Imponendo che sia verificata la condizione di sopra:

$n_1\sin {\theta }_B=n_2\sin (\pi /2-{\theta }_B)=n_2\cos {\theta }_B$

Quindi:

$\tan {\theta }_B=\frac{n_2}{n_1}⟶{\theta }_B={\tan }^{-1}\frac{n_2}{n_1}$

Anche se l'incidenza non è pari all'angolo di Brewster i raggi riflessi sono parzialmente polarizzati. La ragione per cui per evitare di essere abbagliati si usano occhiali con lenti polarizzate che eliminano una componente riflessa.

L'angolo di Brewster è diverso dall'angolo limite o critico. La figura chiarisce la differenza.

Incidenza normale

Per incidenza normale cioè per ${\theta }_i=\pi /2$, non vi è distinzione tra componente parallela e perpendicolare, la riflettanza e la trasmittanza diventano semmplicemente:

$R=R_S=R_P={\left(\frac{n_1-n_2}{n_1+n_2}\right)}^2$

$T=T_S=T_P=1-R=\frac{4n_1{n}_2}{{(n_1+n_2)}^2}$