Fisica matematica/Varietà differenziabili

Introduzione

Sul concetto di varietà differenziabile si basa lo sviluppo della fisica classica e della geometria differenziale. L'idea di base è quella di avere degli oggetti geometrici che localmente siano simili ad ${ℝ}^m$, pur essendo diversi da un punto di vista più globale.

Prima di introdurre tale concetto introduciamo alcune nozioni preliminari.

Definizione (varietà differenziabile)

Definizione (spazio di Hausdorff): uno spazio di Hausdorff è uno spazio topologico $M$ tale che $\mathrm{\forall }x,y\in M$ esistono $U(x)$ e $V(y)$ intorni dei due punti tali che $U\cap V=\mathrm{\varnothing }$

Ora possiamo introdurre il concetto di varietà:

Definizione (varietà differenziabile): una varietà differenziabile (differentiable manifold) è uno spazio topologico di Hausdorff $M,dim(M)=m$ avente una collezione $({𝔘}_{\alpha },{\varphi }_{\alpha })$, chiamate carte, dove ${𝔘}_{\alpha }\subset M$ aperti e le ${\varphi }_{\alpha }:{𝔘}_{\alpha }\to {ℝ}^m$ tali che:

$\bigcup _{\alpha }{𝔘}_{\alpha }=M$

e preso ${𝔘}_{\alpha ,\beta }={𝔘}_{\alpha }\cap {𝔘}_{\beta }\ne \mathrm{\varnothing }$ allora ${\varphi }_{\alpha ,\beta }={\varphi }_{\alpha }\circ {\varphi }_{\beta }^{-1}$ è un diffeomorfismo di ${ℝ}^m$.

Una volta definito le varietà differenziabili vediamo le funzioni: sia $f:M\to ℝ$ una funzione, è possibile definire un rappresentante locale di $f$:

$f_{\alpha }=f\circ {\varphi }_{\alpha }^{-1}:{𝔘}_{\alpha }\to ℝ$. La funzione è detta di classe $C^r$ se il suo rappresentante è differenziabile r volte. L'insieme delle funzioni $C^{\mathrm{\infty }}(ℝ)$ si indica con $𝔉(M)$ e si può dimostrare che forma un anello abeliano grazie alle seguenti operazioni:

somma di funzioni $(f+g)(x)=f(x)+g(x)$ prodotto di funzioni $(fg)(x)=f(x)g(x)$

si vede subito la proprietà distributiva e associativa.

Esempi

Proiezione stereografica della sfera

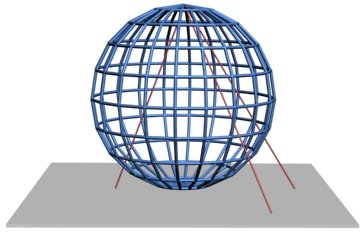
La sfera è uno degli esempi più facili da visualizzare. Il modo più semplice di ricoprire la sfera è quello di costruire delle carte, quattro delle quali servono a mappare i quattro quadranti e le rimanenti due servono a mappare l'equatore e un meridiano (che corrispondono ai punti in cui le carte sono adiacenti).

Utilizzando la proiezione stereografica si può mappare la sfera su un piano e in questo caso bastano solo due carte. Non si può mappare la sfera con una sola mappa, servono sempre almeno due carte.

Un altro esempio di varietà differenziabile è il toro.

Chiaramente non tutte le varietà sono differenziabili, per esempio il cono con la struttura topologica di ${ℝ}^3$ non è una varietà differenziabile a causa della singolarità nell'origine. Esistono altre costruzioni che rendono anche il cono varietà differenziabile.

Definizione (varietà topologica)

Le varietà topologiche non sono varietà differenziabili ma cito la definizione per completezza.

Le varietà topologiche sono definite come le varietà differenziabili ma non richiedono che le funzioni di transizioni siano differenziabili. Risulta ovvio che qualsiasi varietà differenziabile è anche topologica, mentre non vale il viceversa.

Definizione alternativa

La definizione di varietà differenziabile data è abbastanza astratta, si può pensare di dare una definizione più concreta che si basa sulle funzioni di transizioni e su come si possono incollare le toppe della varietà. Template:Avanzamento