Meccanica analitica/Lagrangiana in relatività e l'effetto Compton

La lagrangiana in relatività

L'equazione del moto in meccanica relativistica, ottenuta come:

$\frac{dP}{dt}=F\Rightarrow P=\frac{m_{0}v}{\sqrt{1-\frac{v^2}{c^2}}}$

Può essere espressa nel formalismo lagrangiano, prendendo come variabili generalizzate le variabili cartesiane (o le componenti spaziali nello spazio di Minkowsky). Tuttavia, la definizione di lagrangiana vista finora $L=T-U$ ha poco significato in relatività. Che valore assume $T$? Per questo motivo, si assume come definizione di lagrangiana in relatività l'espressione:

$L=-m_0{c}^2\sqrt{1-\frac{v^2}{c^2}}-V(x)$

Dove, ovviamente, $V(x)$ è l'energia potenziale. Non discuteremo dei motivi per i quali la lagrangiana assume questa forma.

Ricordando che $v^2=\sum _{\alpha =1}^3{v}_{\alpha }^2$, si possono applicare le equazioni di Eulero-Lagrange assumendo come lagrangiana l'espressione scritta sopra per poter ricavare le leggi del moto:

$\frac{d}{dt}\frac{\partial L}{\partial v_{\alpha }}=\frac{\partial L}{\partial x_{\alpha }}$

Abbiamo che:

$\begin{array}{cc}& \frac{\partial L}{\partial v_{\alpha }}=-m_0{c}^2\frac{1}{2\sqrt{1-\frac{v^2}{c^2}}}\cdot (-\frac{2v_{\alpha }}{c^2})=\frac{m_0{v}_{\alpha }}{\sqrt{1-\frac{v^2}{c^2}}}=P_{\alpha }\\ & \frac{\partial L}{\partial x_{\alpha }}=-\frac{\partial V}{\partial x_{\alpha }}=F_{\alpha }\\ \Rightarrow & \frac{\partial P_{\alpha }}{\partial t}=F_{\alpha }\end{array}$

Esattamente come ci aspettavamo.

Effetto Compton

L'esperimento di Compton è successivo all'esperimento fotoelettrico di Einstein (il quale valse a Einstein il Nobel nel 1921); questo aveva dimostrato la natura corpuscolare della luce, studiando l'interazione tra fotoni ed elettroni. Tuttavia, si notò che l'interazione dipendeva non dall'intensità di radiazione, bensì dalla frequenza: fasci di luce molto intensi, a basse frequenze, interagivano poco con gli elettroni di un metallo, a differenza di fasci poco intensi ma con frequenze molto alte, che permettevano agli elettroni di schizzare fuori dal reticolo metallico.

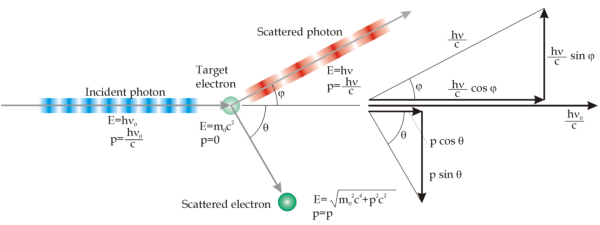
L'effetto Compton (che valse ad Arthur Compton il premio Nobel nel 1927) studia proprio questo effetto: studiando l'energia del fotone come funzione della sua frequenza, si riesce a spiegare l'effetto fotoelettrico. Nell'immagine qui sotto è ben schematizzato l'effetto Compton, con le grandezze di energie relative ad lato di interesse.

Possiamo quindi ricavare una relazione tra l'angolo di scattering del fotone $\varphi$ e la sua frequenza $\nu$, che cambia in ${\nu }^{\prime }$ dopo lo scattering. Sfruttando la conservazione della quantità di moto e dell'energia relativistiche si spiega questo fenomeno. La quantità di moto di un fotone è pari a $P=\frac{h\nu }{c}$, dove $h$ è la costante di Planck di alto interesse e utilizzo in fisica quantistica; l'energia del fotone è proprio $E=h\nu$. Per risolvere il problema, si sfrutta il teorema del coseno:

${\left(\frac{m_{0}v}{\sqrt{1-\frac{v^2}{c^2}}}\right)}^2={\left(\frac{h\nu }{c}\right)}^2+{\left(\frac{h{\nu }^{\prime }}{c}\right)}^2-2\frac{h\nu }{c}\frac{h{\nu }^{\prime }}{c}\cos \varphi$

La conservazione dell'energia, invece, impone, considerata l'energia dell'elettrone come $E=m_o{c}^2$ a riposo, poi come energia in movimento:

$h\nu +m_0{c}^2=h{\nu }^{\prime }+\frac{m_0{c}^2}{\sqrt{1-\frac{v^2}{c^2}}}$

Risolvendo il sistema, si ottiene:

$\begin{array}{cc}& \frac{c}{{\nu }^{\prime }}-\frac{c}{\nu }=\left(\frac{h}{m_{0}c}\right)(1-\cos \varphi )\\ & {\lambda }^{\prime }-\lambda =\frac{h}{m_{0}c}(1-\cos \varphi )\end{array}$

La differenza tra le frequenze del fotone, o tra le rispettive lunghezze d'onda, è quindi in funzione dell'angolo di scattering. La grandezza $\frac{h}{m_{0}c}$ si chiama lunghezza d'onda Compton. Questa lunghezza è equivalente a un fotone avente come energia la stessa energia a riposo della particella: da qui si aprì il dibattito sulla dualità onda-corpuscolo della materia, arrivando poi all'ipotesi di De Broglie. Template:Avanzamento