Matematica per le superiori/Probabilità

La probabilità

Dato un qualsiasi esperimento casuale, i suoi possibili risultati costituiscono gli elementi di un insieme non vuoto, detto spazio campionario che indichiamo con $S$, e ciascun evento è un sottoinsieme di $S$, in pratica un evento è un insieme dei possibili risultati dell'esperimento casuale, ed un risultato dell'esperimento, è un evento elementare. La probabilità è nella sostanza una misura, cioè una funzione che indichiamo con $ℱ$ che associa a ciascun sottoinsieme di eventi un numero reale non negativo tale che la somma delle probabilità di tutti gli eventi sia pari a $1$.

In merito agli eventi possiamo dire che:

- lo spazio campionario $𝒮$ si verifica ad ogni prova e viene detto quindi evento certo

- $\mathrm{\varnothing }$ chiamato insieme vuoto, non si verifica mai e viene quindi detto evento impossibile

- l'evento $𝒜\cup ℬ$ si verifica se si verificano $𝒜,ℬ$ o entrambi.

- l'evento $𝒜ℬ$ si verifica se e solo se si verificano sia $𝒜$ che $ℬ$

- se $𝒜$ si verifica e $𝒜\subset ℬ$ allora anche $ℬ$ si verifica.

Definiamo classe degli eventi $ℱ$ l'insieme di tutti gli eventi. Tutte le operazioni fatte fra eventi danno come risultato ancora un evento quindi $ℱ$ è un campo, o algebra. E poiché sono possibili anche infinite unioni e intersezioni di sequenze infinite di eventi il cui risultato è ancora un evento, allora la classe $ℱ$ è una $\sigma$-algebra.

Se noi ad esempio consideriamo l'esperimento aleatorio consistente nel lancio di un dado, i possibili risultati saranno i numeri riportati sulle sei facce del dado e tutti insieme costituiranno un insieme non vuoto $1,2,3,4,5,6$, in questo esempio i possibili risultati sono anche gli eventi e la somma delle probabilità dei singoli eventi sarà pari ad uno. Se noi ripetiamo un esperimento per un numero $N$ di volte ed indichiamo con $n(ϵ)$ il numero di volte per cui si verifica l'evento $ϵ$, possiamo definire:

$f_N(ϵ):=\frac{n(ϵ)}{N}$

come la frequenza relativa di $ϵ$ su $N$ prove. Tale frequenza è una funzione reale definita come:

$f_N:ℱ\to ℝ$

che gode delle seguenti proprietà:

1. $f_N(S)=1$
2. $f_N(ϵ)\ge 0\mathrm{\forall }ϵ\in ℱ$
3. se $𝒜,ℬ\in ℱ$ sono mutuamente esclusivi $(𝒜ℬ=\varnothing )$ allora $f_N(𝒜\cup ℬ)=f_N(𝒜)+f_N(ℬ)$

Dalla definizione di frequenza relativa possiamo quindi passare alla definizione assiomatica della probabilità.

1. $P(S)=1$
2. $P(ϵ)\ge 0\mathrm{\forall }ϵ\in ℱ$
3. se ${ϵ}_1,{ϵ}_2,...\in ℱ$ sono mutuamente esclusivi (${\mathcal{ϵ}}_{𝒾}{\mathcal{ϵ}}_{𝒿}=\varnothing$ se $i\ne j$) allora $P(\bigcup _{i=1}^{\mathrm{\infty }}{ϵ}_i))=\sum _{i=1}^{\mathrm{\infty }}P({ϵ}_i)$

Vediamo come applicare quanto visto fino ad ora all'esempio del lancio del dado, indichiamo con: $P({ϵ}_i)=\hat{p}$ la probabilità che si verifichi l'evento uscita della faccia $i$ del dado e come funzione $ℱ$ di probabilità quella che assegna uguale probabilità ad ogni evento. Applicando quindi gli assiomi della definizione assiomatica della probabilità si ricava che:

$1=P(S)=P(\bigcup _{i=1}^6{ϵ}_i))=\sum _{i=1}^{6}P({ϵ}_i)=6\hat{p}$

da cui si desume che $\hat{p}=\frac{1}{6}$

Nella sostanza, negli spazi finiti o negli spazi di infiniti numerabili è sufficiente determinare la probabilità degli eventi elementari. Il valore della probabilità di qualsiasi altro evento lo si ricava dalla somma delle probabilità degli eventi elementari.

Conseguenze elementari degli assiomi

(1)

$P(ϵ)=1-P({ϵ}^C)$

da cui desumiamo che

$P(\mathrm{\varnothing })=0$ difatti $\mathrm{\varnothing }=S^C$ per cui $P(\mathrm{\varnothing })=1-P(S)=1-1=0$

(2)

se $𝒜$ e $ℬ$ sono due eventi

$P(𝒜\cup ℬ)=P(𝒜)+P(ℬ)-P(𝒜ℬ)$

considerato che $P(𝒜ℬ)\ge 0$ allora $P(𝒜\cup ℬ)\ge P(𝒜)+P(ℬ)$

(3)

Se $𝒜$ e $ℬ$ sono due eventi con $𝒜\subset ℬ$ allora $P(𝒜)\le P(ℬ)$

Spazi campione uniformi

Gli spazi campione uniformi, sono quegli spazi per cui la probabilità dei singoli eventi è uniforme, ossia sono equiprobabili.

Se $S=\{1,2,...,N\}$ e $P\{1\}=P\{2\}=...=P\{N\}:=\hat{p}$

Dato che $\sum _{i=1}^{N}P\{i\}=1$ questo vuol dire che $N\hat{p}=1$ quindi $\hat{p}=\frac{1}{N}$

Probabilità di un evento in spazi uniformi

Negli spazi uniformi si può definire la probabilità come:

sia $𝒜=\{i_1,i_2,...,i_k\}$ un evento formato da $k$ punti di $S$

allora $P(𝒜)=P(\bigcup _{j=1}^k\{i_j\})=\sum _{j=1}^{k}P\{i_j\}=\frac{k}{N}$

Ad esempio, in un dado sono presenti 6 facce, numerabili da 1 a 6

se $𝒜=\{2,4,6\}$ allora $P(𝒜)=\frac{3}{6}$

Probabilità condizionata

Dato un evento $ℳ$, con probabilità maggiore di zero $P\mathcal{(}ℳ\mathcal{)}>0$ per ogni evento $𝒜$ definiamo probabilità condizionata:

$P\mathcal{(}𝒜\mathcal{|}ℳ\mathcal{)}:=\frac{P\mathcal{(}𝒜ℳ\mathcal{)}}{P\mathcal{(}ℳ\mathcal{)}}$

a cui possiamo dare la seguente interpretazione in frequenza relativa.

Effettuate $n$ prove e posti $n_A,n_M,n_{AM}$ come il numero di occorrenze degli eventi $𝒜,ℳ,𝒜ℳ$

Approssimati

$P(𝒜)\approx \frac{n_A}{n}$

$P(ℳ)\approx \frac{n_M}{n}$

$P(𝒜ℳ)\approx \frac{n_{AM}}{n}$

otteniamo che:

$P\mathcal{(}𝒜\mathcal{|}ℳ\mathcal{)}:=\frac{P\mathcal{(}𝒜ℳ\mathcal{)}}{P\mathcal{(}ℳ\mathcal{)}}\approx \frac{n_{AM}}{n_M}$

Il cui significato è che la probabilità condizionata è uguale alla frequenza relativa dell'evento $𝒜$ considerata solo nella sequenza di prove in cui l'evento $ℳ$ si è verificato.

Appendice

Teoria degli insiemi

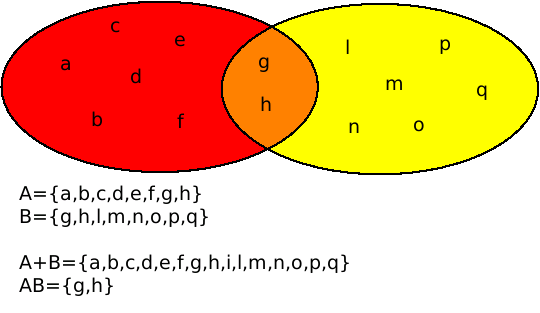
Il diagramma di Venn

Il diagramma di Venn (nome completo diagramma di Eulero-Venn) è una rappresentazione grafica che ha lo scopo di illustrare le operazioni fra insiemi. Consiste in una linea chiusa racchiudente una superficie di forma qualsiasi al cui interno possono sussistere singoli elementi consistenti anche in altri diagrammi di Venn. Questi ultimi possono a loro volta sovrapporsi al fine di racchiudere elementi comuni.

Appartenenza

Sia $a$ un elemento e $𝒜$ un insieme, la notazione $a\in 𝒜$ ha come significato che $a$ appartiene ad $𝒜$ ossia ne è un suo elemento.

Per contro la notazione $a\notin 𝒜$ ha come significato che $a$ non appartiene ad $𝒜$ ossia non ne è un suo elemento.

Inclusione ed uguaglianza

$𝒜\subset ℬ$ ha come significato che ogni elemento di $𝒜$ è anche un elemento di $ℬ$, in pratica $𝒜$ è un sottoinsieme di $ℬ$.

Gli insiemi $𝒜$ e $ℬ$ sono uguali se e solo se ogni elemento dell'insieme $𝒜$ è un elemento dell'insieme $ℬ$ e viceversa.

Ossia deve essere contemporaneamente verificato che:

$𝒜\subset ℬ$

$ℬ\subset 𝒜$

Unione ed intersezione

Definiamo l'unione di due insiemi $𝒜\cup ℬ$ oppure $𝒜\vee ℬ$ l'insieme i cui elementi appartengono ad $𝒜$ a $ℬ$ o a entrambi.

Definiamo intersezione di due insiemi $𝒜\cap ℬ$ oppure $𝒜\wedge ℬ$ l'insieme i cui elementi appartengono sia ad $𝒜$ che a $ℬ$.

$𝒜$ e $ℬ$ sono disgiunti se $𝒜\wedge ℬ=\mathrm{\varnothing }$

Nella notazione corrente è usuale adoperare anche $𝒜+ℬ$ al posto di $𝒜\cup ℬ$ e $𝒜ℬ$ al posto di $𝒜\cap ℬ$

Unione e intersezione godono delle seguenti proprietà:

Commutativa

$𝒜\cup ℬ=ℬ\cup 𝒜$

$𝒜\cap ℬ=ℬ\cap 𝒜$

Associativa

$(𝒜\cup ℬ)\cup 𝒞=𝒜\cup (ℬ\cup 𝒞)$

$(𝒜\cap ℬ)\cap 𝒞=𝒜\cap (ℬ\cap 𝒞)$

Distributiva

$(𝒜\cup ℬ)\cap 𝒞=(𝒜\cap 𝒞)\cup (ℬ\cap 𝒞)$

$(𝒜\cap ℬ)\cup 𝒞=(𝒜\cup 𝒞)\cap (ℬ\cup 𝒞)$

Complemento

Dato $𝒜\subset 𝒮$ definiamo complemento di $𝒜$ rispetto ad $𝒮$ e lo indichiamo con ${𝒜}^C$, l'insieme composto da tutti gli elementi di $𝒮$ che non fanno parte di $𝒜$.

Per il complemento valgono le seguenti proprietà:

$({𝒜}^C{)}^C=𝒜$

$𝒜\cup {𝒜}^C=𝒮$

$𝒜\cap {𝒜}^C=\mathrm{\varnothing }$

Partizione

Una partizione di un insieme $𝒮$, che non sia $\mathrm{\varnothing }$, una classe di sottoinsiemi diversi da $\mathrm{\varnothing }\{{𝒜}_1,{𝒜}_2...,{𝒜}_n\}$, finita o infinita numerabile, che ricopra per intero $𝒮$ senza che vi siano sovrapposizioni.

Deve verificarsi nella sostanza che:

${𝒜}_i{𝒜}_j=\mathrm{\varnothing }\mathrm{\forall }i\ne j$

${𝒜}_1\cup {𝒜}_2\cup ...\cup {𝒜}_n:=\bigcup _{i=1}^n{𝒜}_i=𝒮$

Leggi di De Morgan

$(\bigcup _{i=1}^n{𝒜}_i{)}^C=\bigcap _{i=1}^n{𝒜}_i^C$

$(\bigcap _{i=1}^n{𝒜}_i{)}^C=\bigcup _{i=1}^n{𝒜}_i^C$

Calcolo combinatorio

Disposizioni semplici

Per disposizione semplice di lunghezza $k$ di elementi di un insieme $S$ di $n$ oggetti, con $k\le n$, si intende una presentazione ordinata di $k$' elementi di $S$ nella quale non ci possono essere ripetizioni di uno stesso oggetto.

$D_{n,k}:=n\cdot (n-1)\cdot \dots \cdot (n-k+1)=\frac{n\cdot (n-1)\cdot \dots \cdot 1}{(n-k)\cdot (n-k-1)\cdot \dots \cdot 1}=\frac{n!}{(n-k)!}$

Ad esempio le disposizioni semplici di lunghezza $2$ degli elementi dell'insieme $\{1,2,3,4,5\}$ sono $\frac{5!}{(5-2)!}=\frac{5!}{3!}=\frac{120}{6}=20$

e sono $12,13,14,15,21,23,24,25,31,32,34,35,41,42,43,45,51,52,53,54$

Permutazioni

se $k=n$ le disposizioni semplici si chiameranno permutazioni

$P_n=D_{n,n}:=\frac{n!}{(n-n)!}=\frac{n!}{0!}=\frac{n!}{1}=n!$

Ad esempio le permutazioni di lunghezza $4$ elementi dell'insieme $\{1,2,3\}$ sono $3!=6$

e sono $123,132,213,231,312,321$

Disposizioni con ripetizione

Una disposizione con ripetizioni di $n$ oggetti distinguibili è il numero di possibili sequenze ordinate differenti di $k$oggetti.

$D{\text{'}}_{n,k}=n^k$

Ad esempio le disposizioni con ripetizione di lunghezza $2$ degli elementi di $\{1,2,3,4,5\}$ sono $5^2=25$

$11,12,13,14,15,21,22,23,24,25,31,32,33,34,35,41,42,43,44,45,51,52,53,54,55$

Dove può essere anche $k>n$.

Combinazioni semplici

Una combinazione semplice è una disposizione di elementi che contengono senza ripetizioni gli stessi oggetti presi a gruppi ma in posizioni differenti.

$C_{n,k}=\frac{D_{n,k}}{P_k}=\frac{n!}{k!(n-k)!}=(\genfrac{}{}{0ex}{}{n}{k})$

Ad esempio le combinazioni semplici di lunghezza 4 degli elementi di {1,2,3,4,5,6} sono 6!/(4!2!) = 15: 1234, 1235, 1236, 1245, 1246, 1256, 1345, 1346, 1356, 1456, 2345, 2346, 2356, 2456, 3456.