Propulsione aerea/Capitolo VI°

Moto dei fluidi nei condotti e velocità di efflusso

Supponiamo di avere un serbatoio con un liquido, di densità ρ e peso specifico γ=g ρ alla pressione p₁ e supponiamo di fare effluire questo liquido attraverso un condotto in un ambiente a pressone p₀ (in particolare l'atmosfera). Ammettiamo che il liquido si rinnovi continuamente, in modo qualsiasi, in modo da mantenere inalterata la pressione p₁ e che il condotto sia raccordato ampiamente con la parete del serbatoio; con queste ipotesi avremo un moto permanente con velocità iniziale molto piccola, cioè V₁₌₀. Supposte nulle le perdite per attrito, ecc. il teorema di Bernouille (conservazione dell'energia) applicato per le condizioni iniziali e quelle generiche cioè pressione p e velocità V)

$p_1=\frac{\rho V^2}{2}+p$

permette di calcolare la velocità in funzione del salto di pressione:

$V=\sqrt[2]{\frac{2}{\rho }(p_1-p)}$.

La velocità di efflusso è:

$V_e=\sqrt[2]{\frac{2}{\rho }(p_1-p_0}$.

Indicando con G la portata (peso affluente nell'unità di tempo) si ha per ogni sezione del condotto di area Ω, G=g ρ Ω V=cost.

Ne viene

$\mathrm{\Omega }=\frac{G}{g\rho V}$

cioè la sezione del condotto diminuisce costantemente al crescere di V poiché ρ per i liquidi non varia.

L'ugello di efflusso per i liquidi è quindi convergente.

Supponiamo ora di avere un gas alla pressione p₁ e temperatura T₁ racchiuso nentro un recipiente e lo si faccia effluire con modalità analoghe alle precedenti. L'efflusso sia adiabatico ed isoentropico; trascuriamo le eventuali variazioni di altezza; poiché non vi è scambio di lavoro con l' esterno la relazione di energia (34) in termini finiti fornisce per la sezione generica a temperatura T

$V=\sqrt[2]{2gJ(i_1-i)}=\sqrt[2]{2gJ{C}_p(T_1-T)}$

La velocità ideale di efflusso è

$V_e=\sqrt[2]{2gJ{C}_p(T_1-T_0)}$

per T₀=0(espansione idealmente sino allo zero assoluto) si ha la massima velocità detta limite

$V_{lim}=\sqrt[2]{2gJ{C}_p{T}_1}$.

Data l'isoentropicità per ogni sezione deve aversi:

$p{v}^k=p{v}_1^k$

questa associazione all'equazione di stato fornisce:

$\frac{T}{T_1}=(\frac{\rho }{{\rho }_1}{)}^{k-1}=(\frac{p}{p_1}{)}^{\frac{k-1}{k}}$

si può quindi scrivere indifferente:

$V=\sqrt[2]{2gJ{C}_p{T}_1(1-\frac{T}{T_1})}=\sqrt[2]{2gj{C}_p{T}_1[1-(\frac{\rho }{{\rho }_1}{)}^{k-1}]}=\sqrt[2]{2gJ{C}_p{T}_1[1-(\frac{p}{p_1}{)}^{\frac{k-1}{k}}]}$.

Dall'espressione della portata si ricava sempre:

$\mathrm{\Omega }=\frac{G}{g\rho V}$

L'andamento della sezione dipende da ρ e V entrambi variabili in senso contrario poiché al crescere di V il gas, raffreddandosi, diminuisce di densità; nulla quindi può dirsi a priori sull'andamento della sezione del condotto.

La quantità:

$\rho V=\frac{G}{g\mathrm{\Omega }}=\mathrm{\Phi }$

è il flusso di massa (portata massica riferita all'unità di sezionje); in base alle relazioni precedenti si può quindi scrivere:

$\mathrm{\Phi }={\rho }_1\frac{\rho }{{\rho }_1}\sqrt[2]{2gJ{C}_p{T}_1(1-\frac{T}{T_1})}={\rho }_1\sqrt[2]{2gJ{C}_p{T}_1}\frac{\rho }{{\rho }_1}\sqrt[2]{1-\frac{T}{T_1}}$.

Poiché:

$\frac{\rho }{{\rho }_1}e\frac{T}{T_1}$

non sono indipendenti, ma legati dalle condizioni precedenti, ne viene che il flusso Φ può essere espresso indifferentemente in funzione del rappoorto

$\frac{T}{T_1}oppure\frac{\rho }{{\rho }_1}oppure\frac{p}{p_1}$.

Supponendo Φ espresso in funzione di

$\frac{T}{T_1}=x$

si ha:

${\rho }_1\sqrt[2]{2gJ{C}_p{T}_1}(\frac{T}{T_1}{)}^{\frac{1}{k-1}}\sqrt[2]{1-\frac{T}{T_1}}=\sqrt[2]{x^{\frac{2}{k-1}}-x^{\frac{k+1}{k-1}}}=C\sqrt[2]{x}$.

C congloba tutti i fattori costanti.

Condizioni critiche

Dalla precedente relazione si vede che per x=1 (cioè T=T₁ inizio del condotto) Φ=0 ( cioè il condotto ha sezione molto grande, teoricamente ∞); poiché con l'espansione T diminuisce, x diviene minore dell'unità e tenderebbe a zero quando la T tende allo zero assoluto (ammesso che il gas non passi allo stato liquido); per x=0 si ha quindi nuovamente Φ=0 e szione del condotto →0.

Traquesti estremi deve esserci quindi una sezione di area minima cui corrisponde Φ massimo.

Il massimo del flusso corrisponde al massimo dell'espressione sotto il radicale; derivando ed uguagliando a zero la

$f(x)=x^{\frac{2}{k-1}}-x^{\frac{k+1}{k-1}}$

si trova la condizione di massimo che, ad operazioni eseguite, fornisce:

$x_{cr}=\frac{T_{cr}}{T_1}=\frac{2}{k+1}$

e quindi

${\mathrm{\Phi }}_{max}=C(\frac{k-1}{k+1}{)}^{\frac{1}{2}}(\frac{2}{k+1}{)}^{\frac{1}{k-1}}$

introducendo nell'espressione di V per il T il valore critico

$T_{cr}=T_1\frac{2}{k+1}$

si ricava

$(35)V_{cr}=\sqrt[2]{\frac{k-1}{k+1}2gJ{C}_p{T}_1}$.

La sezione di area minima è chiamata sezione critica; i rispoettivi valori di temperatura, densità, pressione e velocità sono detti pure critici.

Risulta quindi riepilogando:

$\frac{T_{cr}}{T_1}=\frac{2}{k+1}$

$\frac{{\rho }_{cv}}{{\rho }_1}=(\frac{2}{k+1}{)}^{\frac{1}{k-1}}$

$\frac{p_{cr}}{p_1}=(\frac{2}{k+1}{)}^{\frac{k}{k+1}}$

$\frac{V_{cr}}{V_{lin}}=(\frac{k-1}{k+1}{)}^{\frac{1}{2}}$

I valori critici dipendono quindi dalla natura del gas, precisamente dal rapporto:

$k=\frac{C_p}{C_v}$.

Per i gas biatomici e per l'aria (miscuglio di ossigeno ed azoto, gas biatomici, con tracce di gas non biatomici) k=1,4 e risulta in particolare:

$\frac{T_{cr}}{T_1}=0,835\frac{{\rho }_{cr}}{{\rho }_1}=0,633$

$\frac{p_{cr}}{p_1}=0,527\frac{V_{cr}}{V_{lim}}=0,408$.

Inoltre:

${\mathrm{\Phi }}_{max}=0,250C$.

Ugello del Laval-velocità supersoniche

Dalle considerazioni svolte si conclude che se la pressione all'esterno è superiore a quella critica, avanti definita, l'ugello è convergente.

Se inferiore l'ugello è prima vonvergente, sino alla sezione critica e poi divergente; questo ugello è detto anche di De Laval in onore del fisico che per primo chiarì questi aspetti dell'efflusso. Se

$p_0=p_{cr}$

l'ugello si arresta alla sezione critica (fig.22a,b,c).

Vi è dunque nell'efflusso un comportamento diverso tra liquidi e gas proprio a causa della compressibilità.

fig.22a,b,c.......

La velocità locale del suono varia poiché varia la temperatura T secondo la nota formula:

$V_s=\sqrt[2]{gJkRT}=\sqrt[2]{gJ{C}_p(k-1)}T$

Il rapporto tra la velocità ricordando locale della corrente e la velocità locale del suono è il n° di Mach locale; ricordando la posizione

$x=\frac{T}{T_1}$

si trova

$(37)M_{loc}=\frac{V}{V_s}=(\frac{2}{k-1}{)}^{\frac{1}{2}}(\frac{1-x}{x}{)}^{\frac{1}{2}}$

per x=1 (inizio del condotto), M_loc=0 come era da attendersi poiché il gas è fermo.

Per x=0 (velocità di efflusso limite, M_loc=∞; per

$x=\frac{2}{k+1}$

(condizioni critiche), M_loc=1; cioè nella sezione critica la velocità della corrente coincide con la velocità locale del suono; segue inoltre che le velocità a monte della sezione critica sono subsoniche, a valle supersoniche. Risultato importantissimo della gas-dinamica per le applicazioni alle turbine a vapore ed a gas, agli eiettori, alle gallerie aerodinamiche , ai reattori ed autoreattori, agli ugelli dei razzi e dei missili ecc.

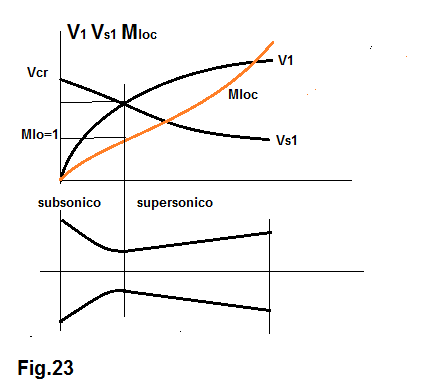
Per maggiore chiarezza in fig,23 sono riportati gli andamenti di V₀, V_s, M_loc, in corrispondenza delle varie sezioni di un ugello di De Laval.

La velocità del suono nelle condizioni iniziali è:

$V_{si}=\sqrt[2]{gj{C}_p(k-1)T_1}$

Ne segue che:

$V_{cr}=({\frac{2}{k+1)}}^{\frac{1}{2}}{V}_{si}$

per k=1,4

$\frac{V_{cr}}{V_{si}}=0,91$

Poiché, come dimostrato, nella parte divergente dell'ugello le velocità sono supersoniche, ne segue che un disturbo qualsiasi non può rimontare la corrente e ripercuotersi avanti all'ostaclo stesso: il suono rimane entro il relativo cono locale di Mach a norma delle considerazioni svolte al Cap.I°.

Riprendiamo la (37) e sostituiamo per x il valore

$\frac{T_0}{T_1}=(\frac{p_0}{p_1}{)}^{\frac{k-1}{k}}$

corrispondente al rapporto di espansione

$\frac{p_1}{p_0}$

Chiamiamo semplicemente M il n di Mach corrispondente, coincidente con quello della corrente generata; si ha:

$(38)\sqrt[2]{\frac{2}{k-1}[(\frac{p_1}{p_0}{)}^{\frac{k-1}{k}}-1]}$.

Questo è il massimo numero di Mach che si può ricavare per il dato rapporto

$\frac{p_1}{p_0}$

Un aspetto, a prima vista strano, è che la portata una volta raggiunte le condizioni critiche non cresce più comunque si faccia piccolo p₀<p_cr,; questo è dovuto pure al fatto, già detto avanti, che la V_cr non è influenzata da quanto succede a valle della sezione critica; al diminuire di p₀ cresce quindi la velocità di efflusso ma non la portata; la portata massima corrisponde a:

${\mathrm{\Phi }}_{max}=(\frac{k-1}{k+1}{)}^{\frac{1}{2}}(\frac{2}{k+1}{)}^{\frac{1}{k-1}}C$

Il calcolo delle velocità può essere fatto rapidamente a mezzo del diagramma di Mollier che allo scopo spesso porta una scala delle velocità in funzione del salto di entropia.

Autocompressione isentropica

Nelle considerazioni precedenti si è fatto riferimento a processi di espansione (corrente accelerata); ma quanto detto in sostanza per l'espansione vale per la compressione spontanea che si ottiene trasformando l'energia cinetica in entalpia (corrente ritardata); così (sempre supponendo il processo isoentropico) per trasformare tut\ta l'energia cinetica in pressione necessita un condotto convergente per velocità subsoniche, prima convergente e poi divergente per velocità supersoniche.

Se la corrente ha il n.di Mach M, dalla (38) si ottiene il rapporto di compressione:

$(39)\frac{p_1}{p_0}=(1+\frac{k-1}{2}{M}^2{)}^{\frac{k}{k-1}}$

es. per l'aria (k=1,4)

$perM=1\frac{p_1}{p_0}=1,2^{3,5}=1,88$

$perM=2\frac{p_1}{p_0}=1,8^{3,5}=7,7$

$perM=3\frac{p_1}{p_0}=2,8^{3,5}=27$.

Sul grafico (24) sono riportati gli andamenti di:

$\frac{p_1}{p_0}e\frac{T_1}{T_0}=1+\frac{k-1}{2}{M}^2$.

Una osservazione si impone; tutta la trattazione e tutte le formule non dicono quale forma debbono avere le sezioni e con quale legge debbono succedersi; in altre parole il condotto può essere allungato od accorciato a piacere e le sezioni comunque variare di forma a parità di area.

In realtà perché il fenomeno non presenti anomalie si richiede che il tratto divergente vari di sezione gradualmente in modo da evitare distacchi di corrente dalle pareti e che le sezioni varino di forma anche esse gradualmente; ordinariamente le sezioni nelle applicazioni concrete hanno forma rettangolare o circolare.

L'angolo di apertura del tratto divergente è sui 12°÷15°; angoli più piccoli, esigendo condotti più lunghi, darebbero luogo a maggiori perdite per attrito.

Onde d'urto

Nelle considerazioni svolte si è ammesso che i parametri fisici p, ρ, T, V varino con continuità e gradualmente entro tutto il campo interessato. Teoria ed esperienza mostrano però che in determinate circostanze i parametri fisici possono variare bruscamente.

I moti subsonici sono caratterizzati proprio dal fatto che p, ρ, T, V, variano gradualmente entro tutto il campo ed alla superficie dei corpi interessati; questa gradualità non si verifica per deflussi transonici e supersonici ed in certe zone del gas si constatano incrementi rilevanti localizzati dei parametri fisici inevitabili per ristabilire le condizioni di continuità; questi incrementi possono essere concepiti, al limite, come vere e proprie discontinuità; pressioni, densità, temperatura e velocità variano quasi a colpo entro spessori molto sottili del gas; queste discontinuità vanno sotto il nome generico di onde d'urto (shoock waves degli anglosassoni). La forma e la distribuzione di queste onde nel caso più generale è funzione dei parametri fisici della corrente k ed M, della forma e dello orientamento rispetto alla corrente dell'ostacolo che interferisce con la corrente.

La gas-dinamica permette di ricavare la distribuzione di queste onde e dimostra che non possono esistere discontinuità di espansione ma soltanto di compressione; attraverso un'onda d'urto la velocità subisce una brusca diminuzione mentre la pressione, la densità e la temperatura subiscono un brusco aumento.

Il fenomeno dell'urto è adiabatico ma non isoentropico; la entro pia del gas aumenta attraverso la discontinuità.

Per la determinazione dei parametri fisici necessitano quattro relazioni. Esse sono in generale: l'equazione della continuità, l'equazione della quantità di moto, l'equazione di stato e l'equazione della conservazione dell'energia.

L'onda d'urto a seconda delle modalità del deflusso può essere obliqua o normale alla direzione della velocità della corrente in arrivo nel posto considerato.

La gas-dinamica fornisce i metodi per lo studio generale delle onde. E' di particolare interesse l'onda d'urto normale alla corrente in arrivo.

Onda d'urto normale

Indicando con l'indice 0 ed 1 i parametri prima e dopo l'onda deve aversi per un tubicino di flusso continuo

$(1){\rho }_0{V}_0={\rho }_1{V}_1$

$(2)p_1-p_0={\rho }_0{V}_0(V_1-V_0)$

$(3)\frac{p_0}{{\rho }_0{T}_0}=\frac{p_1}{{\rho }_1{T}_1}$

$(4)\frac{V_0^2}{2g}+C_p{T}_0=\frac{V_1^2}{2g}+C_p{T}_1$

La (1) si afferisce alla continuità, la (2) alla quantità di moto, la (3) alla equazione di stato e la (4) alla energia.

Risolvendo il sistema precedente è facile, a parte la soluzione banale

$p_0=p_1{\rho }_0={\rho }_1{V}_0=V_1{T}_0=T_1$

che indica assenza dell'urto, trovare il rapporto tra le grandezze dopo e prima dell'urto; si ottiene concisamente se si introduce il numero di Mach M della corrente indisturbata ed il rapporto k:

$(40a)\frac{p_1}{p_0}=\frac{2k{M}^2-(k-1)}{k+1}$

$(40b)\frac{V_1}{V_0}=\frac{{\rho }_0}{{\rho }_1}=\frac{(k+1)}{2+(k-1}$

$(40c)\frac{T_1}{T_0}=\frac{[2k{M}^2-(k-1)][2+(k-1)M^2]}{(k+1{)}^2{M}^2}$.

Si ricava inoltre come conseguenza:

$V_0{V}_1=V_{so}^2$

ed

$M_1^2=\frac{2+(k-1)M^2}{2k{M}^2-(k-1)}$.

Per i gas biatomici k=1,4si ha in particolar

$\frac{p_1}{p_0}=\frac{7M^2-1}{6}$

$\frac{V_1}{V_0}=\frac{{\rho }_0}{{\rho }_1}=\frac{5+M^2}{6M^2}$

$\frac{T_1}{T_0}=(\frac{7M^2-1}{6})(\frac{5+M^2}{6M^2})$

$M_1^2=\frac{5+M^2}{7M^2-1}$

Queste considerazioni sono v alide ovviamente per M>1 cioè per corrente in arrivo supersonica; infatti per M<1 il numero di Mach diviene immaginario e questo conferma che l'urto è possibile per velocità supersoniche solamente.

E' facile vedere inoltre dalle precedenti che si ha sempre M<1, cioè per onda d'urto normale la corrente di velocità V₁ è subsonica mentre quella a velocità V₀ è supersonica.

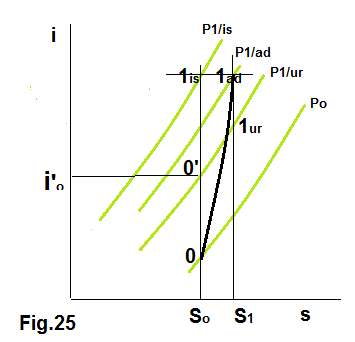
Il punto figurativo 1 delle condizioni del gas dopo l'urto è sulla linea p_1-ur costante (fig.25); esso ha temperatura ed entropia più grandi del punto 0' corrispondente allo stesso rapporto di compressione isoentropica. I valori C_p(T_0'-T₀) e C_p(T_1-ur-T₀) rappresentano rispettivamente il lavoro di compressione isoentropico adiabatico per urto; il rapporto tra questi lavori è il cosi detto rendimento adiabatico η_ad.

Si ha evidentemente :

$(\frac{{T_0}^{\prime }}{T_0}{)}^{\frac{k}{k-1}}=\frac{p_{1,ur}}{p_0}$.

Inoltre l'equazione della linea:

$p_1=cost{e}^{\prime }S-S_0=C_p\log \frac{i}{{i_0}^{\prime }}=C_p\log \frac{T}{{T_0}^{\prime }}$

con

$S_{0}e{C}_p{T_0}^{\prime }={i_0}^{\prime }$

coordinate del punto 0'.

Dalle precedenti si ottiene facilmente l'aumento di entropia ed il rendimento adiabatico per urto normale:

$\mathrm{\Delta }S=S_1-S_0=C_p\log \frac{\frac{T_1}{T_0}}{(\frac{p_1}{p_0}{)}^{\frac{k-1}{k}}}$

${\eta }_{ad}=\frac{{T_0}^{\prime }-T_0}{T_1-T_0}=\frac{(\frac{p_1}{p_0}{)}^{\frac{k-1}{k}}-1}{\frac{T_1}{T_0}-1}$

in queste formule i rapporti

$\frac{p_1}{p_0}e\frac{T_1}{T_0}$

sono quelli dell'urto, avanti precisati.

Autocompressione con urto

Con le formule precedenti si possono calcolare le condizioni subito dopo l'imbocco di una presa dinamica o di un diffusore in corrente supersonica (fig.26); l'onda d'urto normale alla bocca è piana, conica per il resto.

Poiché la corrente V₁ è subsonica è possibile con un condotto divergente trasformare l'energia cinetica

$\frac{V_1^2}{2g}$

in entalpia; se le perdite all'interno del condotto sono trascurabili si ha una ulteriore compressione ad entropia costante S_1; la pressione finale per formule note vale

$\frac{p_{1ad}}{p_1}=(1+\frac{k-1}{2}{M}^2{)}^{\frac{k}{k-1}}$

figura 26

Il rapporto di compressione totale

$\frac{p_{1ad}}{p_0}=\frac{p_{1ad}}{p_1}\frac{p_1}{p_0}$

ottenibile con le trasformazioni avanti indicate; a conti fatti diviene:

$(41)(\frac{p_1}{p_0}{)}_{ad}=\frac{k+1}{2}{M}^2[\frac{(k+1{)}^2{M}^2}{4k{M}^2-2(k-1)}{]}^{\frac{1}{k-1}}$

per k=1,4

$(\frac{p_1}{p_0}{)}_{ad}=1,2M^2(\frac{7,2M^2}{7M^2-1}{)}^{2,5}$.

Se tutto il processo fosse stato isoentropico si sarebbero avute le note espressioni:

$(\frac{p_1}{p_0}{)}_{is}=(1+\frac{k-1}{2}{M}^2{)}^{\frac{k}{k-1}}$

con k=1,4

$(\frac{p_1}{p_0}{)}_{is}=(1+0.2M^2{)}^{3,5}$

Al divergere di M

$(\frac{p_1}{p_0}{)}_{ad}\to 1.2(\frac{7,2}{7}{)}^{2,5}{M}^2=1,28M^2$.

E' poi facile verificare che il rapporto

$(\frac{T_1}{T_0}{)}_{ad}$

è uguale al rapporto

$(\frac{T_1}{T_0}{)}_{is}$

dell'ipotesi isoentropica; questo fatto era da aspettarsi per la conservazione dell'energia; infatti l'energia cinetica non può trasformarsi altro che in entalpia e a parità di temperatura iniziale deve essere quella finale necessariamente uguale sia per il caso entropico che per il caso con urto.

Nella figura 27a,b, sono riportati alcuni valori delle espressioni avanti ricavate.

figura 27a,b

Le minorazioni del rapporto di compressione possono ottenersi agli alti numeri di Mach con bocche ad onde d'urto oblique.

Gli aumenti di entropia con onda d'urto normale sono i più alti possibili. Su qiesto aspetto si ritornerà parlando degli autoreattori supersonici.

Effetti della temperatura e probabili limiti della velocità di volo

Si è visto che per qualsiasi tipo di deflusso, isoentropico o con urto, è valida la relazione:

$(42)\frac{T_1}{T_0}=1+\frac{k-1}{2}{M}^2$

con T₁ temperatura di arresto e T₀ della corrente di Nr.Mach M.

La temperatura T₁ si presenta quindi sui bordi di attacco delle ali, sulla prua delle fusoliere, entro le prese dinamiche dei condotti dei reattori ed autoreattori, ecc.

Per l'aria

$\frac{T_1}{T_0}=1+0,2M^2$.

Per le velocità subsoniche (M<1), l'incremento della temperatura di arresto rispetto a quella ambiente T₀ è moderato; mano a mano che M si avvicina all'unità

$\frac{T_1}{T_0}$

comincia a crescere rapidamente.

Per:

$M=1\frac{T_1}{T_0}=1,2$

cioè si ha l'aumento del 20% della temperatura; se

$T_0=273K(0C)T_1=327K$,

l'aumento è di circa 54°C, nella stratosfera T₀=228°K (-55°C), quindi, T₁=273°K, corrispondente quasi a 0°C.

Per M=2 a bassa quota si ha l'incremento del 80%, pari circa a 218°C e nella stratosfera l'aumento di 182°C.

Sul grafico di fig.28 è riportato l'andamento di

$\frac{T_1}{T_0}$

fiura 28

Al crescere della velocità l'aumento della temperatura comincia ad essere incompatibile con le possibilità del fisico umano innanzitutto; supposto risolto il problema di proteggere l'equipaggio con opportuna refrigerazione, rimane il problema della resistenza dei materiali alle sollecitazioni meccaniche ed alle ossidazioni a caldo.

A 300 °C la resistenza del duralluminio è scesa circa a metà della resistenza a freddo; a bassa quota quindi

$\frac{T_1}{T_0}=\frac{273+300}{273}=2,1$

nella stratosfera

$\frac{T_1}{T_0}=1,93$

a questi valori corrispondono i numeri di Mach pari a circa 2,35 e 2,15, cioè 2800 k/ora e 22300 k/ora circa: però l'ossidazione a caldo limita ancor più questi valori.

Per gli acciai legati inossidabili delle migliori qualità e per le leghe speciali a circa 800 °C (colore rosso chiaro) la resistenza tende a svanire. A queste temperature corrispondono M=4,4 a bassa quota ed M=4,3 nella stratosfera, cioè circa 5400 k/ora e 4400 k/ora; in alte parole alle alte velocità il velivolo od il missile tendono a comportarsi come meteore.

Questi sarebbero quindi, grosso modo, i limiti spinti di velocità nel volo di regime prolungato per i fatti di temperatura nei riguardi della resistenza dei materiali ove non si provveda al raffreddamento artificiale mediante macchine frigorifere o liquidi a bassa temperatura di ebollizione entro opportune intercapedini e condotti a contatto con le superfici esterne dei velivoli.

Da questi cenni si intravede quale somma di ricerche e di lavoro richiede e richiederà il volo supersonico già per la resistenza alle alte temperature del fisico umano e dei materiali.

Naturalmente le considerazioni precedenti si intendono valide per voli sufficientemente lunghi in modo da portare a regime la temperatura delle masse metalliche del velivolo.