Fondamenti di automatica2/Stabilità interna di sistemi dinamici

Template:Fondamenti di automatica2 Lo studio della stabilità interna riguarda gli effetti sul movimento dello stato provocati da perturbazioni dello stato iniziale (l'ingresso rimane costante).

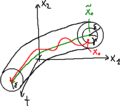
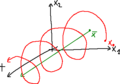
Considerando due evoluzioni temporali dello stato di un sistema dinamico stazionario:

• movimento nominale dello stato $\tilde{x}(\bullet )$: ingresso nominale $\tilde{u}(\bullet )$, stato iniziale nominale ${\tilde{x}}_0$;
• movimento perturbato dello stato $x(\bullet )$: ingresso $u(\bullet )=\tilde{u}(\bullet )$, stato iniziale $x_0\ne {\tilde{x}}_0$.

la perturbazione $\delta x(\bullet )$ dello stato del sistema è la differenza tra i due movimenti, ed è tanto più piccola quanto meno il movimento perturbato si discosta dal movimento nominale:

$\delta x(\bullet )=x(\bullet )-\tilde{x}(\bullet )\in {ℝ}^n$

Un sistema è stabile se il suo movimento non si discosta troppo dal movimento nominale di riferimento a fronte di una piccola perturbazione dello stato iniziale.

Classificazione in base alla stabilità interna

Classificazione dei movimenti nominali in base alla stabilità interna

A fronte di una perturbazione $\delta x_0=x_0-{\tilde{x}}_0$ dello stato iniziale, il movimento nominale $\tilde{x}(\bullet )$ è:

• instabile se la perturbazione $\delta x(\bullet )$ dello stato non resta limitata nel tempo (tipicamente diverge):

  $\mathrm{\forall }\gamma >0:\mathrm{\exists }\epsilon >0⟶\mathrm{\exists }{x}_0:\Vert \delta x_0\Vert \le \gamma ⟹\mathrm{\exists }t\ge 0:\Vert \delta x\left(t\right)\Vert >\epsilon$

• stabile se la perturbazione $\delta x(\bullet )$ dello stato resta limitata nel tempo:
  • semplicemente stabile se la perturbazione $\delta x(\bullet )$ dello stato resta limitata, ma non tende a 0 asintoticamente:

    $\mathrm{\forall }\epsilon >0:\mathrm{\exists }\gamma >0⟶\mathrm{\forall }{x}_0:\Vert \delta x_0\Vert \le \gamma ⟹\{\begin{array}{c}\Vert \delta x\left(t\right)\Vert \le \epsilon ,\mathrm{\forall }t\ge 0\\ \underset{t\to +\mathrm{\infty }}{\lim }\Vert \delta x(t)\Vert =0\end{array}$

  • asintoticamente stabile se la perturbazione $\delta x(\bullet )$ dello stato resta limitata, e tende a 0 asintoticamente:

    $\mathrm{\forall }\epsilon >0:\mathrm{\exists }\gamma >0⟶\mathrm{\forall }{x}_0:\Vert \delta x_0\Vert \le \gamma ⟹\{\begin{array}{c}\Vert \delta x\left(t\right)\Vert \le \epsilon ,\mathrm{\forall }t\ge 0\\ \underset{t\to +\mathrm{\infty }}{\lim }\Vert \delta x(t)\Vert \ne 0\end{array}$

  • globalmente asintoticamente stabile se il movimento nominale $\tilde{x}(\bullet )$ è asintoticamente stabile per qualsiasi perturbazione iniziale:

    $\mathrm{\forall }\epsilon >0:\mathrm{\exists }\gamma >0⟶\mathrm{\forall }{x}_0:\Vert \delta x_0\Vert \le \gamma ⟹\{\begin{array}{c}\Vert \delta x\left(t\right)\Vert \le \epsilon ,\mathrm{\forall }t\ge 0\\ \underset{t\to +\mathrm{\infty }}{\lim }\Vert \delta x(t)\Vert \ne 0,\mathrm{\forall }\delta x_0\in X\end{array}$

• 
  Esempio di movimento instabile
• 
  Esempio di movimento semplicemente stabile
• 
  Esempio di movimento asintoticamente stabile

Stabilità dell'equilibrio

Se il movimento nominale considerato è un punto di equilibrio $(\overline{x},\overline{u})$, si studia la stabilità dell'equilibrio a fronte di perturbazioni dello stato iniziale (l'ingresso rimane pari all'ingresso di equilibrio $\overline{u}$ costante). Ad ogni stato di equilibrio asintoticamente stabile è associata una regione di attrazione o regione di asintotica stabilità: ogni stato iniziale che appartiene alla regione di attrazione dà origine a un movimento perturbato che è asintoticamente stabile.

• 
  Esempio di stato di equilibrio instabile
• 
  Esempio di stato di equilibrio semplicemente stabile
• 
  Esempio di stato di equilibrio asintoticamente stabile