Elaborazione numerica dei segnali/Segnali a tempo discreto

Template:Elaborazione numerica dei segnali L'elaborazione numerica dei segnali (ENS) è l'applicazione di un algoritmo ad una serie di numeri che rappresenta un segnale.

Un segnale $x\left(n{T}_c\right)$ è a tempo discreto se è definito rispetto a una variabile indipendente $n$ che assume solo valori interi ($n\in \mathbb{Z}$). Per semplicità si parla di $x\left(n{T}_c\right)$ come la sequenza $x\left(n\right)$. Il segnale è detto numerico o digitale se assume solo ampiezze discrete.

Classificazione

Durata di una sequenza

Una sequenza può avere:

• durata finita: la sequenza è identicamente nulla all'esterno di un intervallo finito di tempo $[n_1,n_2]$;
• durata infinita: il supporto temporale può essere bilatero ($(-\mathrm{\infty },+\mathrm{\infty })$) o monolatero ($[n_1,+\mathrm{\infty })$ o $(-\mathrm{\infty },n_2)$).

Causalità

Una sequenza è:

• casuale se è identicamente nulla per valori di n minori di 0;
• anticasuale se è identicamente nulla per valori di n maggiori o uguali di 0.

Parità

Una sequenza $x\left(n\right)$ reale è detta:

• pari se $x\left(n\right)=x(-n)$;
• dispari se $x\left(n\right)=-x(-n)$.

Una sequenza $x\left(n\right)$ complessa è detta:

• coniugata simmetrica se $x\left(n\right)=x^{*}(-n)$;
• coniugata antisimmetrica se $x\left(n\right)=-x^{*}(-n)$.

Una qualunque sequenza complessa $x\left(n\right)$ può essere scritta come somma di una sequenza coniugata simmetrica $x_p\left(n\right)$ e di una sequenza coniugata antisimmetrica $x_d\left(n\right)$:

$x\left(n\right)=x_p\left(n\right)+x_d\left(n\right)$

dove:

$\{\begin{array}{c}{x}_p\left(n\right)=\frac{1}{2}x\left(n\right)+\frac{1}{2}{x}^{*}(-n)=x_p^{*}(-n)\\ x_d\left(n\right)=\frac{1}{2}x\left(n\right)-\frac{1}{2}{x}^{*}(-n)=-x_d^{*}(-n)\end{array}$

Periodicità

Una sequenza $x\left(n\right)$ è periodica se è possibile trovare un intervallo di tempo $N$ per cui vale la relazione:

$x\left(n\right)=x(n\pm N)N\in \mathbb{N}$

Il periodo è il più piccolo valore intero positivo di $N$ per cui la sequenza è periodica.

Sequenze limitate in ampiezza

Una sequenza $x\left(n\right)$ è limitata se per qualunque istante di tempo discreto $n$ assume valori contenuti entro un intervallo finito $X_0$ (costante reale finita positiva):

$\left|x\left(n\right)\right|\le X_0\mathrm{\forall }n$

Sequenze sommabili

Una sequenza $x\left(n\right)$ è assolutamente sommabile se:

$\sum _{n=-\mathrm{\infty }}^{+\mathrm{\infty }}\left|x\left(n\right)\right|\in ℝ$

Una sequenza $x\left(n\right)$ è quadraticamente sommabile se:

$\sum _{n=-\mathrm{\infty }}^{+\mathrm{\infty }}{\left|x\left(n\right)\right|}^2\in ℝ$

Sequenze elementari

Sequenza gradino unitario

$u\left(n\right)=\{\begin{array}{cc}0,& n<0\\ 1,& n\ge 0\end{array}$ Template:Clear

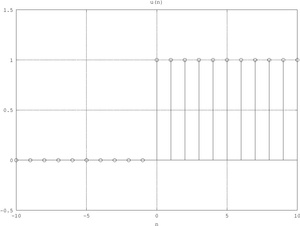
Delta di Kronecker (impulso unitario)

$\delta \left(n\right)=\{\begin{array}{cc}0,& n\ne 0\\ 1,& n=0\end{array}$

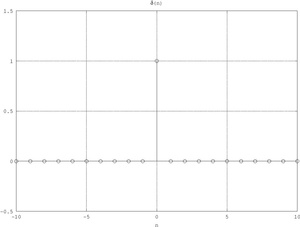
Qualsiasi segnale $x\left(n\right)$ può essere espresso come somma di impulsi:

$x\left(n\right)=\sum _{i=-\mathrm{\infty }}^{+\mathrm{\infty }}x\left(i\right)\delta (n-i)$

Relazione tra delta numerica e gradino unitario

$u\left(n\right)=\sum _{i=0}^{+\mathrm{\infty }}\delta (n-i)=\delta \left(n\right)+\delta (n-1)+\delta (n-2)+\dots$

$\delta \left(n\right)=u\left(n\right)-u(n-1)$

Sequenza rampa

$r\left(n\right)=nu\left(n\right)=\{\begin{array}{cc}0,& n<0\\ n,& n\ge 0\end{array}$ Template:Clear

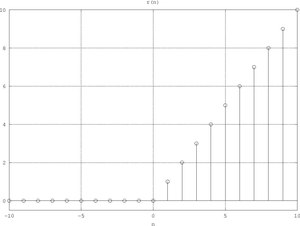
Sequenza sinc

$\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\left(\frac{n}{N}\right)=\frac{\sin \left(\pi \frac{n}{N}\right)}{\pi \frac{n}{N}},N\in \mathbb{N}$

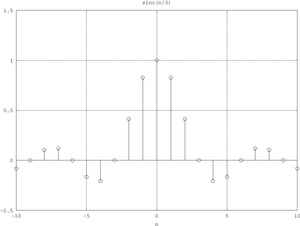
Interseca l'asse orizzontale in $N$, $2N$, ecc.

Se $N=1$, la sequenza $\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\left(n\right)$ coincide con la delta di Kronecker. Template:Clear

Sequenza triangolo

$t_{2N+1}\left(n\right)=\{\begin{array}{cc}1-\frac{\left|n\right|}{N},& \left|n\right|\le N\\ 0,& \left|n\right|>N\end{array},N\in \mathbb{N}$ Template:Clear

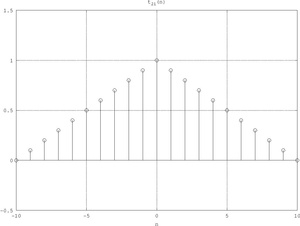
Sequenza esponenziale

$x\left(n\right)=a^{n}u\left(n\right)$

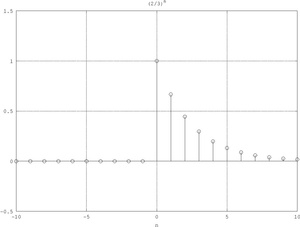
Se $a$ è complesso:

$a=A{e}^{j\theta }\Rightarrow x\left(n\right)=A^n{e}^{jn\theta }u\left(n\right)$

Sinusoidi a tempo discreto

Proprietà 1

Sinusoidi che differiscono per un numero intero di angoli giro sono indistinguibili nel dominio del tempo discreto:

$A\cos (2\pi f_{0}n+2\pi kn+\theta )=A\cos (2\pi f_{0}n+\theta )k\in \mathbb{Z}$

Proprietà 2

La frequenza delle oscillazioni di una sinusoide a tempo discreto:

• $0<f_0<\frac{1}{2}$: aumenta all'aumentare di $f_0$;
• $\frac{1}{2}<f_0<1$: diminuisce all'aumentare di $f_0$.

Proprietà 3

Una sinusoide è periodica se il prodotto $N{f}_0$ è un numero intero:

$x(n+N)=x\left(n\right)\Rightarrow A\cos (2\pi f_{0}n+2\pi f_{0}N+\theta )=\cos (2\pi f_{0}n+\theta )N\in \mathbb{Z}$

Una sinusoide discreta perciò non necessariamente è periodica di periodo $\frac{1}{f_0}$. Se $f_0$ non è un numero razionale, la sinusoide non è periodica ($N$ dev'essere intero).

Operazioni elementari

Somma e prodotto

Le operazioni di somma e prodotto si applicano tra coppie di campioni osservati nei medesimi istanti di tempo.

Traslazione e ribaltamento

Traslazione

La traslazione consiste nel campio di variabile $n\to n-N$, dove $N\in \mathbb{N}$ è pari al numero di campioni per cui il segnale è ritardato o anticipato:

$y\left(n\right)=x(n-N)$

Ribaltamento

Il ribaltamento consiste nel cambio di variabile $n\to -n$ e realizza l'inversione dell'asse dei tempi:

$y\left(n\right)=x(-n)$

L'operazione di traslazione ha la precedenza su quella di ribaltamento:

$x\left(n\right)\to x(n-N)\to x(-n-N)$

Scalamento temporale

Sottocampionamento

L'operazione di sottocampionamento corrisponde a costruire la sequenza $y\left(n\right)$ prendendo un campione ogni $D$ della sequenza $x\left(n\right)$:

$y\left(n\right)=Dx\left(n\right)D\in \mathbb{N}$

Corrisponde all'operazione di compressione nel dominio del tempo continuo. La funzione Matlab è downsample.

Sovracampionamento

L'operazione di sovracampionamento corrisponde a costruire la sequenza $y\left(n\right)$ inserendo $I-1$ zeri tra ogni campione della sequenza $x\left(n\right)$:

$y\left(n\right)=\{\begin{array}{cc}x\left(\frac{n}{I}\right)& \mathrm{\forall }n=\dots ,-2I,-I,0,+I,+2I,\dots \\ 0& \text{altrimenti}\end{array}$

Corrisponde all'operazione di dilatazione nel dominio del tempo continuo. La funzione Matlab è upsample.

Convoluzione lineare

La convoluzione lineare tra due sequenze discrete $x\left(n\right)$ e $y\left(n\right)$ è definita:

$x\left(n\right)*y\left(n\right)=\sum _{k=-\mathrm{\infty }}^{+\mathrm{\infty }}x\left(k\right)y(n-k)$

Proprietà

Il supporto della convoluzione è pari alla somma dei singoli supporti meno 1.

• commutativa:

  $x\left(n\right)*y\left(n\right)=y\left(n\right)*x\left(n\right)$

• distributiva:

  $x\left(n\right)*[y\left(n\right)+z\left(n\right)]=x\left(n\right)*y\left(n\right)+x\left(n\right)*z\left(n\right)$

• associativa:

  $x\left(n\right)*[y\left(n\right)*z\left(n\right)]=[x\left(n\right)*y\left(n\right)]*z\left(n\right)$

La funzione Matlab è conv.

Energia e potenza media

Energia

$E_x=\sum _{n=-\mathrm{\infty }}^{+\mathrm{\infty }}{\left|x\left(n\right)\right|}^2$

Per sequenze a energia finita, l'energia non dipende da traslazioni temporali di $x\left(n\right)$:

$E_x=\sum _{n=-\mathrm{\infty }}^{+\mathrm{\infty }}{\left|x\left(n\right)\right|}^2=\sum _{n=-\mathrm{\infty }}^{+\mathrm{\infty }}{\left|x(n-N)\right|}^2\mathrm{\forall }N\in \mathbb{Z}$

L'energia di un segnale analogico $x\left(t\right)$ è approssimabile alla sua sequenza $x\left(n{T}_c\right)$ campionata a intervalli $T_c$ molto piccoli:

$E_x=\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}{\left|x\left(t\right)\right|}^{2}dt\approx T_c\sum _{n=-\mathrm{\infty }}^{+\mathrm{\infty }}{\left|x\left(n{T}_c\right)\right|}^2$

Potenza media

Per sequenze a energia infinita è possibile definire la potenza media:

$P_x=\underset{N\to \mathrm{\infty }}{\lim }\frac{1}{2N+1}\sum _{n=-N}^{+N}{\left|x\left(n\right)\right|}^2$

• Le sequenze a energia finita hanno potenza media nulla.
• Le sequenze a potenza media finita (e non nulla) hanno energia infinita.

Esempio

La sequenza gradino unitario $u\left(n\right)$ ha energia infinita ma potenza media finita:

$E_x=\sum _{n=-\mathrm{\infty }}^{+\mathrm{\infty }}{\left|u\left(n\right)\right|}^2=\sum _{n=0}^{+\mathrm{\infty }}1\to +\mathrm{\infty }$

$P_x=\underset{N\to +\mathrm{\infty }}{\lim }\frac{1}{2N+1}\sum _{n=-N}^{+N}{\left|u\left(n\right)\right|}^2=\underset{N\to +\mathrm{\infty }}{\lim }\frac{1}{2N+1}\sum _{n=0}^{+N}1=\underset{N\to +\mathrm{\infty }}{\lim }\frac{N+1}{2N+1}=\frac{1}{2}$

La potenza media di un segnale periodico è pari alla potenza media calcolata in un suo periodo. La potenza media $P_x$ di un segnale periodico dipende dall'energia del segnale all'interno di un singolo periodo:

$P_x=\frac{1}{N}\sum _{n=0}^{N-1}{\left|x\left(n\right)\right|}^2$

La potenza di un segnale analogico $x\left(t\right)$ è approssimabile alla sua sequenza $x\left(n{T}_c\right)$ campionata a intervalli $T_c$ molto piccoli:

$P_x=\underset{T\to +\mathrm{\infty }}{\lim }\frac{1}{2T}\underset{-T}{\overset{T}{\int }}{\left|x\left(t\right)\right|}^{2}dt\cong \underset{N\to +\mathrm{\infty }}{\lim }\frac{1}{(2N+1)\cancel{T_c}}\sum _{n=-N}^{+N}{\left|x\left(n{T}_c\right)\right|}^2\cancel{T_c}$

Inoltre, se il segnale è periodico:

$P_x=\frac{1}{T}\underset{0}{\overset{T}{\int }}{\left|x\left(t\right)\right|}^{2}dt\cong \frac{1}{N\cancel{T_c}}\sum _{n=0}^{N-1}{\left|x\left(n{T}_c\right)\right|}^2\cancel{T_c}$

Funzioni di correlazione

	Mutua correlazione	Autocorrelazione
	$R_{xy}\left(n\right)=\sum _{k=-\mathrm{\infty }}^{+\mathrm{\infty }}{x}^{*}(k+n)y\left(k\right)$	$R_x\left(n\right)=\sum _{k=-\mathrm{\infty }}^{+\mathrm{\infty }}{x}^{*}(k+n)x\left(k\right)$
Sequenze a potenza finita	${\mathrm{\Phi }}_{xy}\left(n\right)=\underset{N\to +\mathrm{\infty }}{\lim }\frac{1}{2N+1}\sum _{k=-N}^{+N}{x}^{*}(k+n)y\left(k\right)$	${\mathrm{\Phi }}_x\left(n\right)=\underset{N\to +\mathrm{\infty }}{\lim }\frac{1}{2N+1}\sum _{k=-N}^{+N}{x}^{*}(k+n)x\left(k\right)$
Sequenze periodiche	${\mathrm{\Phi }}_{xy}\left(n\right)=\frac{1}{N}\sum _{k=0}^{N-1}{x}^{*}(k+n)y\left(k\right)$	${\mathrm{\Phi }}_x\left(n\right)=\frac{1}{N}\sum _{k=0}^{N-1}{x}^{*}(k+n)x\left(k\right)$
Proprietà	se la sequenza è reale: $R_{xy}\left(n\right)=R_{yn}(-n)$	$R_x\left(0\right)=\sum _{k=-\mathrm{\infty }}^{+\mathrm{\infty }}{\left|x\left(k\right)\right|}^2=E_x$

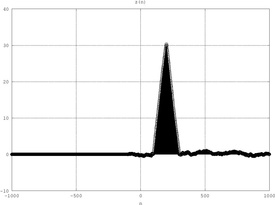
Esempio: segnale radar

La funzione di mutua correlazione può essere usata per ricavare informazioni sul grado di similarità tra due sequenze a energia finita.

L'eco $r\left(n\right)$ di un segnale radar $x\left(t\right)$ è del tipo:

$r\left(n\right)=\alpha x(n-D)+g\left(n\right)$

• $\alpha$ è l'attenuazione del segnale;
• $D$ è il ritardo del segnale;
• $g\left(n\right)$ è il rumore.

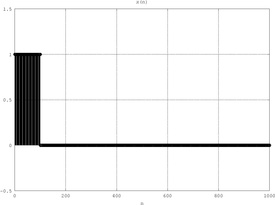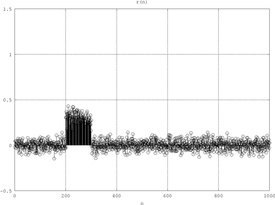La funzione di mutua correlazione $z\left(n\right)$ ha un picco in $n=D$ → sapendo il ritardo è possibile calcolare la distanza dell'oggetto: $d=\frac{D}{2}\cdot c$.

$x\left(n\right)$

$r\left(n\right)$

$z\left(n\right)$