Esercizi di fisica con soluzioni/Correnti alternate

Esercizi

1. Circuito RC in corrente alternata

Consideriamo un generatore di corrente alternata come in figura che funziona a $\nu =50Hz$, $V_{eff}=220V$ con in serie una resistenza $R=1k\mathrm{\Omega }$, $C=1\mu F$ . Determinare la corrente $I_{eff}$, la tensione efficace ai capi della resistenza $R$ e del condensatore $C$ e lo sfasamento tra corrente ${\phi }_1$ e generatore, tra $V_R(t)$ e generatore, tra $V_C(t)$ e generatore.

2. Circuito RL in corrente alternata

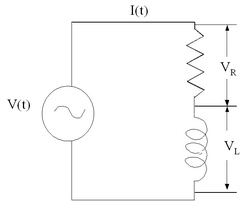
Consideriamo un generatore di corrente alternata come in figura che funziona a $\nu =50Hz$, $V_{eff}=220V$ con in serie una resistenza $R=1k\mathrm{\Omega }$, $L=0.5H$ . Determinare la corrente $I_{eff}$, la tensione efficace ai capi della resistenza $R$ e dell'induttanza $L$ e lo sfasamento tra corrente ${\phi }_1$ e generatore, tra $V_R(t)$ e generatore, tra $V_L(t)$ e generatore.

3. Motore in corrente alternata

Un motore in corrente alternata si può rappresentare come una induttanza con in serie una resistenza. Il motore è alimentato a una presa normale di abitazione ($\nu$, $V_{eff}$). Se la potenza assorbita dal motore è $P_m$ (Potenza media), e vi è uno sfasamento di ${\theta }_0$ tra corrente e tensione. Determinare:

a) L'impedenza totale del motore.

b) La resistenza e l'induttanza del motore.

c) Il valore della capacità di rifasamento, cioè una capacità da porre in serie al circuito in maniera da diminuire lo sfasamento portandolo a ${\theta }_1$.

(dati del problema $\nu =50Hz$, $V_{eff}=220V$, ${\theta }_0=-60^o$, ${\theta }_1=-20^o$, $P_m=150W$)

4. Circuito RCL in corrente alternata

Un circuito RCL serie è alimentato alla frequenza di risonanza. Nella induttanza può al massimo scorrere una corrente $I_0$. In tale condizione estrema determinare:

a) La differenza di potenziale massima ai capi dei vari elementi circuitali.

b) L'energia fornita in un periodo dal generatore.

c) La frequenza per cui la differenza di potenziale ai capi dell'induttanza sia due volte quella ai capi della capacità.

(dati del problema $I_0=1A$, $R=10\mathrm{\Omega }$, $L=10mH$, $C=100nF$)

5. Circuito RCRL in corrente alternata

Un circuito costituito da una resistenza $R_1$in parallelo con un condensatore $C$, in serie con un resistenza $R_2$ ed una induttanza $L$.

a) Determinare percentualmente quanto la frequenza di risonanza esatta si discosti da quella approssimata.

b) L'impedenza del circuito alla frequenza di risonanza.

c) Il fattore di merito del circuito.

(dati del problema $R_1=1000\mathrm{\Omega }$, $L=10\mu H$, $C=100nF$, $R_2=1\mathrm{\Omega }$)

6. Limite circuito risonante

Un circuito è costituito da una resistenza $R$ in parallelo con un condensatore $C$ ed in serie una induttanza $L$. In quali limiti il circuito può considerarsi un circuito risonante?

Se in particolare la resistenza vale $R=1k\mathrm{\Omega }$ quanto vale il fattore di merito?

(dati del problema $C=1\mu F$, $L=0.1mH$)

7. Solenoide ruotante

Un solenoide di raggio $r$, lunghezza $l$, di $N$ spire, ruota con velocità angolare $\omega =10^{3}rad/s$ costante attorno ad un asse normale al suo asse di simmetria e passante per il centro del solenoide. Se esso è immerso in un campo magnetico uniforme il cui vettore di induzione magnetica è diretto all'istante iniziale lungo l'asse del solenoide con intensità $|B|$.

a) Determinare il valore efficace della forza elettromotrice indotta ai capi del solenoide.

b) Se viene chiuso su una resistenza $R$ (grande rispetto alla resistenza del filo del solenoide che quindi si trascura) quanto vale la potenza media dissipata (l'induttanza del solenoide non è trascurabile a queste frequenze).

(dati del problema $r=7mm$, $l=15cm$, $N=1200$, $|B|=10^{-3}T$, $R=1.5\mathrm{\Omega }$, $\omega =10^{3}rad/s$)

8. Circuito risonante con 2 R

Consideriamo un generatore di corrente alternata come in figura. L'ampiezza del generatore vale $V_o=1mV$ con in serie una resistenza $R_1=0.001\mathrm{\Omega }$, una induttanza $L=1\mu H$ e in serie un condensatore $C=1\mu F$ con in parallelo la sua resistenza di perdita $R_2$ che può avere tre valori $10k\mathrm{\Omega }$, $1k\mathrm{\Omega }$ e $10M\mathrm{\Omega }$.

Determinare la frequenza di risonanza, il fattore di merito e la tensione ai capi della capacità nei tre casi: detti a), b) e c).

9. Circuito risonante con 2 C

Il circuito mostrato in figura è composto di un generatore in tensione alternata di ampiezza costante e pulsazione variabile:

$V(t)=V_0\cos (\omega t)$

La maglia è composta di una induttanza $L$ e due condensatori in serie il primo, con perdite, rappresentate dalla resistenza $R$ in parallelo, ed il secondo di capacità $\alpha C$ praticamente senza perdite.

a) Determinare la frequenza ${\nu }_R$ per cui la corrente efficace nella maglia sia massima

b) Il valore di tale corrente efficace.

c) Il valore del fattore di merito $Q$, di valore elevato, ipotesi che si può verificare a posteriori.

Suggerimento: dai dati numerici l'intervallo di interesse è quello per cui $\omega RC\gg 1$, approssimare i conti ove possibile tenendo conto di tale fatto.

(dati del problema: $\alpha =100$, $C=1nF$, $L=1H$, $R=100M\mathrm{\Omega }$, $V_o=1V$).

10. Trasformatore con carico

Un generatore di tensione alternata a $\omega$ con tensione efficace $V_{eff}$ è collegato ad un trasformatore come in figura.

Determinare la potenza fornita dal generatore per i due valori di $R_2$ dati.

(dati del problema $\omega =50Hz$, $V_{eff}=220V$, $L_1=L_2=M=20H$, $R_1=1\mathrm{\Omega }$, $R_{2a}=10\mathrm{\Omega }$, $R_{2b}=10k\mathrm{\Omega }$)

11. Luce da palcoscenico

Il circuito mostrato in figura è lo schema del funzionamento di una lampada da palcoscenico. La funzione dell'induttanza variabile (indicata in figura dal simbolo dell'induttanza con una freccia sovrapposta) è di variare la potenza dissipata in media nella lampada (indicata dalla resistenza) e quindi la sua luminosità.

Il generatore di tensione alternata alla frequenza $\nu$ ha una ampiezza $V_0$. Determinare: a) il valore di $R$ sapendo che quando $L=0$ la potenza media dissipata dalla resistenza vale $P_0$; b) la potenza media dissipata quando l'induttanza assume il suo valore massimo $L_{\mathrm{m}\mathrm{a}\mathrm{x}}$.

(dati del problema $\nu =50Hz$, $V_0=310V$, $P_0=1000W$, $L_{\mathrm{m}\mathrm{a}\mathrm{x}}=0.8H$)

12. Circuito RC

Determinare il valore della frequenza per cui lo sfasamento tra corrente è tensione nella maglia è $\phi$ ed a tale frequenza determinare la potenza media fornita dal generatore. Con $V_e$ si indica il valore della tensione efficace del generatore in corrente alternata.

(dati del problema $\phi =30^o$, $V_e=220V$, $C=1nF$, $R=10\mathrm{\Omega }$ )

13. Circuito risonante parallelo

Il circuito mostrato in figura è alimentato con un generatore $V_{eff}=1.1V$ di cui può essere variata la frequenza. L'induttanza vale $L=1.2mH$, la capacità vale $C=10\mu F$, le due resistenze $R_1=80\mathrm{\Omega }$ e $R_2=10\mathrm{\Omega }$. Determinare: a) la corrente efficace fornita dal generatore se la pulsazione vale ${\omega }_1=100rad/s$; b) la tensione efficace ai capi di $R_1$ per una pulsazione ${\omega }_2=10^{6}rad/s$; c) la pulsazione di risonanza; d) l'impedenza alla frequenza di risonanza.

(se è possibile approssimare non fare conti esatti)

14. Circuito risonante oscillante

Il circuito mostrato è costituito da un condensatore di capacità $C=1\mu F$ che prima di aprire l'interruttore ha una carica $Q_0=10\mu C$. Mentre l'induttanza vale $L=0.1mH$ e la resistenza vale $R=1\mathrm{\Omega }$. Determinare a) l'andamento della carica in funzione del tempo e in particolare dopo uno pseudoperiodo; b) l'andamento della corrente nella maglia nel tempo e in particolare dopo un 1/4 di pseudoperiodo (dove la corrente raggiunge il primo massimo); c) la percentuale di energia persa in 1/4 di pseudoperiodo.

15. Circuito RLC smorzato

Il circuito mostrato è costituito da un condensatore di capacità $C=1\mu F$ che prima di aprire l'interruttore ha una carica $Q_0=10\mu C$. Mentre l'induttanza vale $L=0.1mH$ e la resistenza vale $R=1k\mathrm{\Omega }$. Determinare : a) l'andamento della carica in funzione del tempo e a $t=1ms$; b) l'andamento della corrente nella maglia nel tempo e a $t=1ms$; c) la percentuale di energia persa dopo $t=1ms$.

Soluzioni

1. Circuito RC in corrente alternata

Soluzione:

L'equazione della maglia è (eliminando la variabile tempo esplicitamente dall'equazione):

$V=IR+\frac{I}{j\omega C}$

$I=\frac{V}{R-\frac{j}{\omega C}}$

Quindi:

$I_{eff}=\frac{V_{eff}}{\sqrt{R^2+\frac{1}{(\omega C{)}^2}}}=0.066A$

Per quanto riguarda lo sfasamento tra corrente e generatore:

$I=\frac{V}{R^2+\frac{1}{(\omega C{)}^2}}(R+\frac{j}{\omega C})$

quindi dall'algebra dei numeri complessi:

${\phi }_1=\arctan \frac{1}{\omega CR}=72^o$

Quindi:

$V_R=RI$

$V_{Reff}=I_{eff}R=66V$

Lo sfasamento con il generatore è lo stesso della corrente, essendo $R$ un numero reale. Mentre:

$V_c=\frac{I}{j\omega C}$

$V_{Ceff}=\frac{I_{eff}}{\omega C}=210V$

In questo caso:

$V_c=\frac{V}{R^2+\frac{1}{(\omega C{)}^2}}\frac{1}{j\omega C}(R+\frac{j}{\omega C})=\frac{V}{R^2+\frac{1}{(\omega C{)}^2}}(-j\frac{R}{\omega C}+\frac{1}{{\omega }^2{C}^2})$

Quindi lo sfasamento tra tensione ai capi del condensatore e generatore vale:

${\phi }_2=-\arctan (\omega CR)=-17^o$

Se la frequenza diminuisse la parte della impedenza dovuta alla capacità in serie aumenterebbe al limite rendendo trascurabile la resistenza: il circuito diventerebbe molto simile ad un semplice condensatore, la tensione ai capi della resistenza sarebbe trascurabile: un circuito di questo genere, si usa per elimare le basse frequenze e si chiama infatti taglia basso. Notiamo come la pulsazione che delimita il passaggio tra la bassa e l'alta frequenza è quella per cui le due impedenze in modulo si equivalgono:

$R=\frac{1}{\omega C}$ cioè:

$\omega =\frac{1}{RC}=1000rad/s$

$\nu =159Hz$ Quindi a $50Hz$ la frequenza è bassa.

2. Circuito RL in corrente alternata

L'equazione della maglia è (eliminando la variabile tempo esplicitamente dall'equazione):

$V=IR+j\omega LI$

$I=\frac{V}{R+j\omega L}$

Quindi:

$I_{eff}=\frac{V_{eff}}{\sqrt{R^2+(\omega L{)}^2}}=0.217A$

Per quanto riguarda lo sfasamento tra la corrente I(t) (in fase con Vr) e la tensione V(t) del generatore si ha:

$I=\frac{V}{R^2+{\omega }^2{L}^2}(R-j\omega L)$

quindi dall'algebra dei numeri complessi:

${\phi }_1=-\arctan \frac{\omega L}{R}=-9^o$

Quindi:

$V_R=RI$

$V_{Reff}=I_{eff}R=217V$

Lo sfasamento tra V(t) e Vl si ottiene come segue:

$V_L=j\omega LI=\frac{V\omega L}{R^2+{\omega }^2{L}^2}(jR+\omega L)$

$V_{Leff}=\omega L{I}_{eff}=34V$

Quindi lo sfasamento tra la tensione V(t) del generatore e la tensione Vl ai capi di L è:

${\phi }_3=\arctan \left(\frac{R}{\omega L}\right)=81^o$

Se la frequenza aumentasse la parte della impedenza dovuta alla induttanza in serie aumenterebbe al limite rendendo trascurabile la resistenza: il circuito diventerebbe molto simile ad un semplice induttore, la tensione ai capi della resistenza sarebbe trascurabile.

3. Motore in corrente alternata

definendo $\omega =2\pi \nu$

a) Essendo:

$P_m=V_{eff}{I}_{eff}\cos {\theta }_0$

$I_{eff}=\frac{P_0}{V_{eff}\cos {\theta }_0}=1.36A$

$Z=\frac{V_{eff}}{I_{eff}}=\frac{V_{eff}^2\cos {\theta }_0}{P_0}=161\mathrm{\Omega }$

b)

Quindi:

$R=Z\cos {\theta }_0=81\mathrm{\Omega }$

ed $\omega L=-Z\sin {\theta }_0=140\mathrm{\Omega }$ $L=0.44H$

c)

L'impedenza totale nel caso della capacità di rifasamento vale:

$Z=\frac{R}{\cos {\theta }_1}=86\mathrm{\Omega }$

questo vuol dire che:

${(\omega L-\frac{1}{\omega C})}^2+R^2=Z^2$

Eliminando la soluzione $-(\omega L-\frac{1}{\omega C})=\sqrt{Z^2-R^2}$

Che corrisponde a ${\theta }_1>0$, escluso dai dati del problema. Rimane:

$(\omega L-\frac{1}{\omega C})=\sqrt{Z^2-R^2}$

da cui:

$\frac{1}{\omega C}=\omega L-\sqrt{Z^2-R^2}$

$C=\frac{1}{\omega (\omega L-\sqrt{Z^2-R^2})}=29\mu F$

4. Circuito RCL in corrente alternata

a) La corrente che scorre alla risonanza, per cui il generatore fornisce una

$I_{0}R=f_{max}=10V$

ai capi della resistenza vi sono quindi $V_R=10V$ mentre detta:

${\omega }_r=\frac{1}{\sqrt{LC}}=3\cdot 10^{4}rad/s$

La tensione ai capi del condensatore vale:

e ovviamente la stessa ai capi dell'induttanza:

$V_L=I_0{\omega }_{r}L=316V$

b)

La potenza media vale:

$P_m=I_0{f}_{max}/2=5W$

quindi in un periodo:

$T=\frac{2\pi }{{\omega }_r}$

da cui:

$E=993\mu J$

c)

Basta imporre che:

$2\frac{I_x}{{\omega }_{x}C}=I_x{\omega }_{x}L$

${\omega }_x=\sqrt{2}{\omega }_r$

${\nu }_x=\sqrt{2}{\omega }_r/2\pi =7.11kHz$

5. Circuito RCRL in corrente alternata

a)

L'impedenza totale del circuito vale:

$Z_{tot}=R_2+j\omega L+\frac{1}{1/R_1+j\omega C}=R_2+j\omega L+\frac{R_1}{1+j\omega R_{1}C}=R_2+j\omega L+\frac{R_1(1-j\omega R_{1}C)}{1+{\omega }^2{R}_1^2{C}^2}$

la parte immaginaria vale:

$Z_{imm}=\omega L-\frac{\omega R_1^{2}C}{1+{\omega }^2{R}_1^2{C}^2}$

che si annulla per:

${\omega }_r=9.9995\cdot 10^{5}rad/s$

mentre la pulsazione approssimata di risonanza vale:

${\omega }_a=\frac{1}{\sqrt{LC}}=1\cdot 10^{6}rad/s$

quindi:

$\frac{{\omega }_r-{\omega }_a}{{\omega }_a}=-0.005\mathrm{\%}$

b)

$Z_r=R_2+\frac{R_1}{1+{\omega }_r^2{R}_1^2{C}^2}=1.1\mathrm{\Omega }$

c)

$Q=\frac{{\omega }_{r}L}{Z_r}=9.1$

6. Limite circuito risonante

La parte reale dell'impedenza vale:

$Z_R=\frac{R}{1+{\omega }^2{C}^2{R}^2}$

Mentre quella immaginaria:

$Z_{imm}=\omega L-\frac{\omega C{R}^2}{1+{\omega }^2{C}^2{R}^2}$

La parte immaginaria si annulla se:

$\omega =\frac{1}{RC}\sqrt{\frac{C{R}^2}{L}-1}$

Cioè solo se:

$\frac{C{R}^2}{L}>1$

$R>10\mathrm{\Omega }$

In questo caso specifico con $R=1k\mathrm{\Omega }$:

${\omega }_R=10^{5}rad/s$

$Z_R=0.1\mathrm{\Omega }$

ed il fattore di merito vale:

$Q=\frac{{\omega }_{R}L}{Z_R}=100$

7. Solenoide ruotante

a) Il flusso che attraversa ogni spira del solenoide vale:

$\varphi =|B|\pi r^2\cos \omega t$

Quindi dalla legge di Faraday-Newman-Lentz applicata al solenoide di $N$ spire:

$V=-\frac{d\varphi }{dt}=N{B}_o\pi r^2\omega \sin \omega t$

$V_{eff}=\frac{N{B}_o\pi r^2\omega }{\sqrt{2}}=131mV$

b) L'induttanza del solenoide vale:

$L={\mu }_o\frac{N^2}{l}\pi r^2=1.85mH$

L'impedenza totale del circuito vale:

$Z=j\omega L+R$

Quindi la corrente efficace:

$I_{eff}=\frac{V_{eff}}{|Z|}=\frac{V_{eff}}{\sqrt{{\omega }^2{L}^2+R^2}}=55mA$

Lo sfasamento tra corrente e tensione vale:

$\phi =-\arctan \frac{\omega L}{R}=-0.89rad$

Quindi della potenza totale dissipata:

$P_{tot}=I_{eff}{V}_{eff}\cos \phi =4.5mW$

8. Circuito risonante con 2 R

L'impedenza del parallelo tra capacità e resistenza $R_2$ vale:

$1/Z_p=j\omega C+\frac{1}{R_2}$

$Z_p=\frac{R_2}{1+{\omega }^2{C}^2{R}_2^2}-j\frac{\omega C{R}_2^2}{1+{\omega }^2{C}^2{R}_2^2}$

Quindi la parte reale dell'impedenza vale:

$Z_R=R_1+\frac{R_2}{1+{\omega }^2{C}^2{R}_2^2}$

mentre la immaginaria:

$Z_{imm}=\omega L-\frac{\omega C{R}_2^2}{1+{\omega }^2{C}^2{R}_2^2}$

La immaginaria si annulla se:

$\omega L-\frac{\omega C{R}_2^2}{1+{\omega }^2{C}^2{R}_2^2}=0$

cioè se:

$L=\frac{C{R}_2^2}{1+{\omega }_r^2{C}^2{R}_2^2}$

${\omega }_r=\sqrt{\frac{C{R}_2^2}{L}-1}\frac{1}{C{R}_2}$

ma essendo in tutti e tre i casi:

$C{R}_2^2/L\gg 1$ (nel caso b) vale $1E6$) si ha che trascurando nella radice $1$ rispetto a $C{R}_2^2/L$.

${\omega }_r\approx \frac{1}{\sqrt{LC}}=10^{6}rad/s$

Alla frequenza di risonanza la parte reale vale:

$Z_R=R_1+\frac{R_2}{1+{\omega }_r^2{C}^2{R}_2^2}$

In questo caso si ha che: a) $Z_R=0.0011\mathrm{\Omega }$, b) $Z_R=0.002\mathrm{\Omega }$ e c) $Z_R=0.001$

Quindi essendo il fattore di merito:

$Q=\frac{{\omega }_{r}L}{Z_R}$

nei tre casi vale:

a) $Q=909$, b) $Q=500$ e c) $Q=1000$

La corrente massima che scorre nel circuito alla risonanza vale:

$I_o=\frac{V_o}{Z_R}$

nei tre casi vale: a) $I_o=0.909A$, b) $I_o=0.5A$ e c) $I_o=1A$

La corrente nel nodo vale:

$I_o=I_c+I_R$

Con $I_c$ corrente nella capacità e $I_R$ nel ramo della resistenza $R_2$ (entrambe in genere immaginarie al contrario di $I_o$), inoltre:

$\frac{I_c}{j\omega C}=I_R{R}_2$

Quindi, combinando le due equazioni e approssimando ${\omega }_r^2{C}^2{R}_2^2+1\approx {\omega }_r^2{C}^2{R}_2^2$ si ha che:

$I_c=I_o[1+j/({\omega }_{r}C{R}_2)]\approx I_o$

trascurando il termine immaginario, quindi la tensione ai capi del condensatore vale:

$V_c=\frac{I_o}{j{\omega }_{r}C}$

che vale in modulo:

$|V_c|=\frac{I_o}{\omega C}$

nei tre casi vale: a) $V_c=0.909V$, b) $V_c=0.5V$ e c) $V_c=1V$

9. Circuito risonante con 2 C

L'impedenza totale della maglia utilizzando l'algebra dei numeri complessi:

$Z_{tot}=j\omega L+\frac{1}{1/R+j\omega C}+\frac{1}{j\omega \alpha C}=Z_R+j{Z}_{imm}$

dove:

$Z_{imm}=\omega L-\frac{\omega R^{2}C}{1+{\omega }^2{R}^2{C}^2}-\frac{1}{\omega \alpha C}$

$Z_R=\frac{R}{1+{\omega }^2{R}^2{C}^2}$

quando siamo in bassa frequenza:

$\omega RC\ll 1$

$Z_R\approx R$

Quindi la parte reale è costante.

Mentre quella immaginaria:

$Z_{imm}\approx \omega L-\omega R^{2}C-\frac{1}{\omega \alpha C}$

diverge a bassa frequenza essendo nel nostro caso:

$L\ll R^{2}C$

Ad alta frequenza invece:

$\omega RC\gg 1$

$Z_R\approx \frac{1}{{\omega }^{2}R{C}^2}$

mentre la parte immaginaria:

$Z_{imm}\approx \omega L-\frac{1}{\omega C}-\frac{1}{\omega \alpha C}$

è composto da una induttanza $L$ ed una capacità equivalente:

$C_{eq}=\frac{1}{1/C+1/(\alpha C)}=\frac{\alpha C}{\alpha +1}$

a)

Quindi la pulsazione di risonanza:

${\omega }_R=\sqrt{\frac{\alpha +1}{\alpha LC}}=3.18\cdot 10^{4}rad/s$

la frequenza di risonanza:

${\nu }_R=\frac{{\omega }_R}{2\pi }=5kHz$

b)

A tale frequenza la parte immaginaria si annulla quindi rimane solo la parte reale:

$I_{eff}=\frac{V_{eff}}{Z_R}=\frac{V_0}{\sqrt{2}}{\omega }_R^{2}R{C}^2=0.07A$

c)

Il fattore di merito vale:

$Q=\frac{{\omega }_{R}L}{Z_R}=31780$

10. Trasformatore con carico

Il circuito equivalente è mostrato in figura. Quindi l'impedenza vista dal generatore è:

$Z=R_1+\frac{j\omega M{R}_2}{j\omega M+R_2}$

Razionalizzando:

$Z=R_1+\frac{j\omega M{R}_2(R_2-j\omega M)}{{\omega }^2{M}^2+R_2^2}$

Quindi la parte immaginaria vale:

$Z_i=\frac{j\omega M{R}_2^2}{{\omega }^2{M}^2+R_2^2}$

e quella reale:

$Z_r=R_1+R_2\frac{{\omega }^2{M}^2}{{\omega }^2{M}^2+R_2^2}$

Lo sfasamento vale:

$\phi =-\arctan \frac{Z_i}{Z_r}$

Mentre:

$|Z|=\sqrt{Z_i^2+Z_r^2}$

Quindi essendo:

$I_{eff}=\frac{V_{eff}}{|Z|}$

La potenza vale:

$P=I_{eff}{V}_{eff}\cos \phi$

nei due casi (sostituendo i dati numerici):

$P_a=1.63kW$

$P_b=6.3W$

11. Luce da palcoscenico

a)

L'ampiezza della corrente vale:

$I_R=\frac{V_o}{R+j\omega L}$

Se $L=0$ la potenza dissipata è semplicemente:

$P_o=\frac{V_o^2}{2R}$

quindi:

$R=\frac{V_o^2}{2P_o}=48\mathrm{\Omega }$

b)

Mentre se $L=L_{max}$:

$V_e=\frac{V_o}{\sqrt{2}}=220V$

$I_e=\frac{V_e}{\sqrt{R^2+{\omega }^2{L}_{max}^2}}=0.86A$

mentre lo sfasamento tra corrente e tensione vale:

$\phi =-\arctan \frac{\omega L_{max}}{R}=-79^o$

quindi:

$P_d=V_e{I}_e\cos \phi =35W$

12. Circuito RC

L'equazione della maglia con il metodo simbolico è:

$V=IR+\frac{I}{j\omega C}$

Dall'algebra dei numeri complessi:

$\tan \phi =\frac{1}{\omega CR}$

$\omega =\frac{1}{\tan \phi CR}$

$\nu =\frac{\omega }{2\pi }=\frac{1}{2\pi \tan \phi CR}=27MHz$

Quindi:

$I_e=\frac{V_e}{\sqrt{R^2+1/(\omega C{)}^2}}=19A$

Quindi la potenza media fornita dal generatore vale:

$P_m=V_e{I}_e\cos \phi =3630W$

13. Circuito risonante parallelo

a)

La pulsazione ${\omega }_1$ è piccola essendo ${\omega }_{1}L\ll R_2$ e $1/({\omega }_{1}C)\gg R_2$, per cui il parallelo è praticamente la sola resistenza $R_2$ e quindi la corrente vale:

$I_{1e}\approx \frac{V_{eff}}{R_1+R_2}=12.2mA$

b)

La pulsazione ${\omega }_2$ è grande essendo ${\omega }_{2}L\gg R_2$ e $1/({\omega }_{2}C)\ll {\omega }_{2}L$, per cui il parallelo è l'impedenza della sola capacità che molto piccola, quindi la caduta di potenziale è solo ai capi di $R_2$ ed è:

$V_{R_2}\approx V_{eff}=1.1V$

c)

Usando il metodo simbolico, l'impedenza totale vista dal generatore è:

$Z=R_1+\frac{1}{j\omega C+1/(R_2+j\omega L)}=R_1+\frac{R_2+j\omega L}{1-{\omega }^{2}LC+j\omega R_{2}C}$

Razionalizzando la frazione:

$Z=R_1+\frac{(R_2+j\omega L)(1-{\omega }^{2}LC-j\omega R_{2}C)}{(1-{\omega }^{2}LC{)}^2+(\omega R_{2}C{)}^2}$

Annullando il numeratore della parte immaginaria:

$\omega L-{\omega }^3{L}^{2}C-\omega R_2^{2}C=0$

${\omega }_r=\sqrt{1/(LC)-R_2^2/L^2}=3700rad/s$

d)

$Z_R=R_1+\frac{R_2}{(1-{\omega }_r^{2}LC{)}^2+({\omega }_r{R}_{2}C{)}^2}=92\mathrm{\Omega }$

14. Circuito risonante oscillante

Le condizioni iniziali del problema sono: $Q(t=0)=Q_0$ e $I(t=0)=0$.

Mentre l'equazione della maglia è:

$\frac{Q}{C}=RI+L\frac{dI}{dt}$

Essendo: $I=-dQ/dt$ si può anche scrivere:

$L\frac{d^{2}Q}{d{t}^2}+R\frac{dQ}{dt}+\frac{Q}{C}=0$

La soluzione generica di una equazione differenziale di questo genere è la combinazione lineare di due soluzioni esponenziali, infatti sostituendo a $Q$ una generica $A{e}^{\alpha t}$ si ha che la equazione differenziale diventa equivalente a :

$L{\alpha }^{2}A{e}^{\alpha t}+R\alpha A{e}^{\alpha t}+\frac{A{e}^{\alpha t}}{C}=0$

Che quindi diventa una equazione di II grado in $\alpha$:

$L{\alpha }^2+R\alpha +\frac{1}{C}=0$

le cui soluzioni sono:

${\alpha }_1=-\frac{R}{2L}+\sqrt{\frac{R^2}{4L^2}-\frac{1}{LC}}$

${\alpha }_2=-\frac{R}{2L}-\sqrt{\frac{R^2}{4L^2}-\frac{1}{LC}}$

Le due soluzioni non sono reali in quanto:

$\frac{R^2}{4L}<\frac{1}{C}$

quindi se definiamo: $\omega =\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}=10^{5}rad/s$ (cioè $\omega \approx \sqrt{1/(LC)}$) e $\tau =\frac{2L}{R}=0.2ms$ La soluzione generale è:

$Q(t)=Q_o{e}^{-t/\tau }[\cos (\omega t)+\frac{1}{\tau \omega }\sin (\omega t)]$

Si definisce pseudoperiodo $T=2\pi /\omega$ e quindi:

$Q(T)=Q_o{e}^{-T/\tau }=7.3\mu C$

b)

La corrente è data da:

$I(t)=-dQ/dt=\frac{Q_o}{\tau }{e}^{-t/\tau }[\cos (\omega t)+\frac{1}{\tau \omega }\sin (\omega t)]-Q_o{e}^{-t/\tau }[-\omega \sin (\omega t)+\frac{1}{\tau }\cos (\omega t)]$

$I(t)=Q_o{e}^{-t/\tau }(\omega -\frac{1}{{\tau }^2\omega })\sin (\omega t)\approx Q_o{e}^{-t/\tau }\omega \sin (\omega t)$

Chiaramente il seno ha un massimo quando $\omega t=\pi /2$ cioè per $t=T/4$:

$I(T/4)=0.92A$

c)

L'energia iniziale vale:

$E_o=\frac{Q_o^2}{2C}=50\mu J$

Mentre l'energia immagazzinata nella induttanza dopo $T/4$ vale:

$E_f=\frac{1}{2}LI(T/4{)}^2=42.5\mu J$

Quindi la variazione percentuale vale:

$DE=\frac{E_f-E_o}{E_o}100=-15\mathrm{\%}$

In realtà al tempo $T/4$ vi è della carica nella capacità:

$Q(T/4)=Q_o{e}^{-T/4\tau }\frac{1}{\tau \omega }=0.46\mu C$

Quindi vi anche una energia immagazzinata:

$E_c=\frac{Q(T/4{)}^2}{2C}=0.1\mu J$

trascurabile rispetto a quella nella induttanza.

15. Circuito RLC smorzato

Le condizioni iniziali del problema sono: $Q(t=0)=Q_0$ e $I(t=0)=0$.

Mentre l'equazione della maglia è:

$\frac{Q}{C}=RI+L\frac{dI}{dt}$

Essendo: $I=-dQ/dt$ si può anche scrivere:

$L\frac{d^{2}Q}{d{t}^2}+R\frac{dQ}{dt}+\frac{Q}{C}=0$

La soluzione generica di una equazione differenziale di questo genere è la combinazione lineare di due soluzioni esponenziali, infatti sostituendo a $Q$ una generica $A{e}^{\alpha t}$ si ha che la equazione differenziale diventa equivalente a :

$L{\alpha }^{2}A{e}^{\alpha t}+R\alpha A{e}^{\alpha t}+\frac{A{e}^{\alpha t}}{C}=0$

Che quindi diventa una equazione di II grado in $\alpha$:

$L{\alpha }^2+R\alpha +\frac{1}{C}=0$

le cui soluzioni sono:

${\alpha }_1=-\frac{R}{2L}+\sqrt{\frac{R^2}{4L^2}-\frac{1}{LC}}$

${\alpha }_2=-\frac{R}{2L}-\sqrt{\frac{R^2}{4L^2}-\frac{1}{LC}}$

Le due soluzioni sono reali in quanto:

$\frac{R^2}{4L^2}>\frac{1}{LC}$

Detti ${\tau }_1=-1/{\alpha }_1=1ms$ e ${\tau }_2=-1/{\alpha }_2=0.1\mu s$ La carica nel tempo vale:

$Q(t)=Q_{10}{e}^{-t/{\tau }_1}+Q_{20}{e}^{-t/{\tau }_2}$

Mentre la corrente:

$I(t)=\frac{Q_{10}}{{\tau }_1}{e}^{-t/{\tau }_1}+\frac{Q_{20}}{{\tau }_2}{e}^{-t/{\tau }_2}$

Imponendo le condizioni iniziali:

$Q_{10}+Q_{20}=Q_0$

$\frac{Q_{10}}{{\tau }_1}+\frac{Q_{20}}{{\tau }_2}=0$

segue che:

$Q_{10}=\frac{Q_0}{1-{\tau }_2/{\tau }_1}=10.0001\mu C\approx Q_0$

$Q_{20}=-Q_0\frac{{\tau }_2}{{\tau }_1}=-1nC\approx 0$

a)

Quindi:

$Q(t_1)=3.68\mu C$

b)

$I(t_1)=3.7mA$

c)

L'energia iniziale vale:

$E_o=\frac{Q_o^2}{2C}=50\mu J$

Dopo $1ms$ nel condensatore vi è:

$E_c=\frac{Q(t_1{)}^2}{2C}=6.8\mu J$

Mentre l'energia immagazzinata nella induttanza è trascurabile:

$E_m=\frac{1}{2}LI(t_1{)}^2=0.68nJ$

Quindi la variazione percentuale vale:

$DE=\frac{E_c-E_o}{E_o}100=-86\mathrm{\%}$