Algebra vettoriale/Integrali

Integrali

In questo capitolo ci occuperemo dei differenti tipi di integrali che si presentano quando si trattano funzioni che hanno a che fare con scalari e vettori e introdurremo alcune nozioni associate. Quando si ha a che fare con funzioni vettoriali di uno scalare, come $\overrightarrow{𝒜}(t)$, c'è un solo integrale da considerare. Quando ci si occupa di funzioni scalari o vettoriali di un vettore,quali le funzioni di posizione $\varphi (\overrightarrow{𝓇})$ e $\overrightarrow{𝒜}(\overrightarrow{𝓇})$, dobbiamo distinguere tra integrali di linea, di superficie e di volume. Template:Avanzamento

Integrazione di una funzione vettoriale di uno scalare

Se un vettore $\overrightarrow{𝒜}$ è funzione di una variabile scalare t, si può formare il così detto integrale indefinito

$\int \overrightarrow{𝒜}(t)dt$

nello stesso modo come si forma la integrazione di uno scalare (integrazione di una funzione scalare funzione di una variabile scalare). Il risultato della integrazione è un'altre funzione vettoriale dello scalare t, che è determinata nei limiti di una costante additiva e che è, generalmente un vettore. Scrivamo quindi

$\int \overrightarrow{𝒜}dt=\overrightarrow{ℬ}(t)+\overrightarrow{𝒞}$

Ne consegue che

$\frac{d\overrightarrow{ℬ}}{dt}=\overrightarrow{𝒜}(t)$

Se la variabile t varia continuamente da un particolare valore t₁ ad un altro particolare valore t₂ l'integrale

$\underset{t_1}{\overset{t_2}{\int }}\overrightarrow{𝒜}(t)dt$

è l'integrale definito di $\overrightarrow{𝒜}$ tra i limiti t₁ e t₂. Template:Avanzamento

Integrali di linea

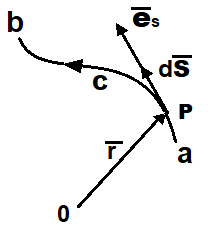
Si consideri una funzione scalare di posizione $\varphi =\varphi (\overrightarrow{𝓇})$ ed il campo da essa descritto. In un tale campo C rappresenti una curva tracciata da un punto a ad un punto b. Si assegni alla curva una direzione di percorrenza come quella spostamento dal punto a al punto b. Poniamo che $\overrightarrow{𝓇}$ denoti la posizione da qualche origine di un punto P sulla curva e che $d\overrightarrow{𝓈}$ denoti un elemento di lunghezza lungo la curva dal punto P. Se $\overrightarrow{{ℯ}_{𝓈}}$ è un versore tangente alla linea nel punto P, si ha che $d\overrightarrow{𝓈}=ds\overrightarrow{{ℯ}_{𝓈}}$. L'integrale
$\underset{a}{\overset{b}{\int }}\varphi (\overrightarrow{𝓇})d\overrightarrow{𝓈}$
o l'equivalente
$\underset{a}{\overset{b}{\int }}\varphi (\overrightarrow{𝓇})\overrightarrow{{ℯ}_{𝓈}}ds$
preso lungo la curva C è chiamato integrale di linea. Il valore di questo integrale è un vettore.

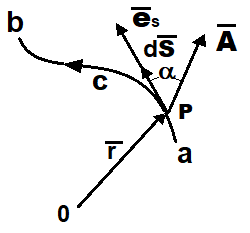
Ora consideriamo una funzione vettoriale di posizione $\overrightarrow{𝒜}(\overrightarrow{𝓇})$. Se C e una linea curvilinea come prima può venire formato un integrale di linea
$\underset{a}{\overset{b}{\int }}\overrightarrow{𝒜}\cdot d\overrightarrow{𝓈}$

oppure $\underset{a}{\overset{b}{\int }}\overrightarrow{𝒜}\cdot \overrightarrow{{ℯ}_{𝓈}}ds$

lungo la curva C tra i punti estremi dati. L'integrale è semplicemente l'integrale lungo C delle componenti di $\overrightarrow{𝒜}$ tangenti alla curva. Se, come mostra la figura, $\alpha$ è l'angolo tra $\overrightarrow{{ℯ}_{𝓈}}$ ed $\overrightarrow{𝒜}$, questo integrale può pure venire riscritto
$\underset{a}{\overset{b}{\int }}Acos\alpha ds$

in cui A è la grandezza di $\overrightarrow{𝒜}$. Il risultato di questo integrale è uno scalare. In genere questo integrale di linea. come qualunque altro integrale di linea, dipende dalla funzione $\overrightarrow{𝒜}(\overrightarrow{𝓇})$, il sentiero lungo il quale l'integrale viene computato ed i punti terminali della linea. Tuttavia, sotto certe condizioni, il valore dell'integrale dipende soltanto dai punti limite estremi e diventa indipendente dal tracciato di curva che li unisce.

Notiamo che un altro integrale di linea di $\overrightarrow{𝒜}(\overrightarrow{𝓇})$ può venire impostato come segue

$\underset{a}{\overset{b}{\int }}\overrightarrow{𝒜}(\overrightarrow{𝓇})\times d\overrightarrow{𝓈}oppure\underset{a}{\overset{b}{\int }}\overrightarrow{𝒜}(\overrightarrow{𝓇})\times \overrightarrow{{ℯ}_{𝓈}}ds$
il risultato di questo integrale è un vettore.

Circolazione

Gli integrali di linea del tipo appena descritto possono essere formati lungo delle linee curve chiuse. Di particolare interesse è l'ntegrale
$\oint \overrightarrow{𝒜}\cdot d\overrightarrow{𝓈}oppure\oint \overrightarrow{𝒜}\cdot \overrightarrow{{ℯ}_{𝓈}}dsoppure\oint Acos\alpha ds$
lungo una curva spaziale C. Un tale integrale è noto come circolazione vettoriale del vettore $\overrightarrow{𝒜}$ lungo la curva C. Generalmente, il valore della circolazione è diverso da zero e dipende dalla funzione $\overrightarrow{𝒜}(\overrightarrow{𝓇})$ e dalla curva C. In taluni casi, tuttavia, la circolazione svanisce e risulta indipendente dalla curva.

integrale di superficie

Si prenda in considerazione una superficie non chiusa S tracciata in un campo descritto da una funzione di posizione scalare $\varphi (\overrightarrow{𝓇})$. Si divida la superficie in elementi infinitesimali. Ciascuno degli elementi della superficie può venire ora considerato come una superficie piana e denotato come un vettore

$d\overrightarrow{𝒮}=\overrightarrow{𝓃}dS$

laddove $\overrightarrow{𝓃}$ è un versore normale all'elemento di superficie. Il versore $\overrightarrow{𝓃}$ è tracciato arbitrariamente da un lato o dall'altro della superficie S. Tuttavia, se prima viene assegnato un verso di circolazione lungo il perimetro C della superficie, la direzione di $\overrightarrow{𝓃}$ viene scelta secondo la regola della mano destra a seconda del verso di percorso lungo C. Impiegando queste notazioni diamo forma all'integrale

$\underset{S}{\iint }\varphi (\overrightarrow{𝓇})d\overrightarrow{𝒮}oppure\underset{S}{\iint }\varphi (\overrightarrow{𝓇})\overrightarrow{𝓃}dS$

sull'intera superficie S. Un tale integrale è nominato integrale di superficie della funzione $\varphi$ sulla superficie S. Il risultato dell'integrale è un vettore.
Consideriamo il prossimo vettore funzione di posizione $\overrightarrow{𝒜}(\overrightarrow{𝓇})$ e poniamo che S sia una superficie aperta nel suo campo. Allora l'integrale
$\underset{S}{\iint }\overrightarrow{𝒜}\cdot dSoppure\underset{S}{\iint }\overrightarrow{𝒜}\cdot \overrightarrow{𝓃}dS$
comwputato sulla superficie S è nominato integrale di superficie di $\overrightarrow{𝒜}$sulla superficie S. Poiché $\overrightarrow{𝒜}\cdot \overrightarrow{𝓃}$ è la componente di $\overrightarrow{𝒜}$ nella direzione della normale all'elemento di superficie, questo integrale è semplicemente l'integrale di superficie di questa componente. Il valore di questo integrale è quindi uno scalare.

Per il campo vettoriale $\overrightarrow{𝒜}(\overrightarrow{𝓇})$ si può formare un altro integrale espresso da
$\underset{S}{\iint }\overrightarrow{𝒜}(\overrightarrow{𝓇})\times d\overrightarrow{𝒮}oppure\underset{S}{\iint }\overrightarrow{𝒜}(\overrightarrow{𝓇})\times \overrightarrow{𝓃}dS$
Il risultato di un tale integrale è un vettore

Integrali di superficie descritti sopra possono venire pure composti su superfici chiuse. Come mostrato nella figura sia S una superficie chiusa e, come prima, si ponga che $d\overrightarrow{𝒮}=\overrightarrow{𝓃}dS$ denoti un elemento di S. Per una superficie chiusa, la normale sarò sempre tracciata in tale modo che esca dalla regione racchiusa dalla superficie e ci si riferirà ad essa come la normale uscente. Facendo uso di questa convenzione diamo forma ai seguenti integrali di superficie.
$\underset{S.c}{\iint }\varphi d\overrightarrow{𝒮}oppure\underset{S.c}{\iint }\varphi \overrightarrow{𝓃}dS$
Il risultato di questo integrale è un vettore.
Per un campo vettoriale $\overrightarrow{𝒜}(\overrightarrow{𝓇})$
$\underset{S.c}{\iint }\overrightarrow{𝒜}\cdot d\overrightarrow{𝒮}oppure\underset{S.c}{\iint }\overrightarrow{𝒜}\cdot \overrightarrow{𝓃}dS$

il risultato del quale è uno scalare.
L'altto integrale è

$\underset{S.c}{\iint }\overrightarrow{𝒜}\times d\overrightarrow{𝒮}oppure\underset{S.c}{\iint }\overrightarrow{𝒜}\times \overrightarrow{𝓃}dS$
I risultato del quale è un vettore.
Questi ultimi tre integrali si presentano frequentemente nei problemi di fisica.

Flusso di un vettore uscente da una superficie

La quantità $\overrightarrow{𝒜}\cdot d\overrightarrow{𝒮}oppure\overrightarrow{𝒜}\cdot \overrightarrow{𝓃}dS$ è abitualmente chiamata flusso di un vettore $\overrightarrow{𝒜}$ uscente da un elemento superficiale $d\overrightarrow{𝒮}$. Con flusso uscente di $\overrightarrow{𝒜}$ intendiamo il flusso di $\overrightarrow{𝒜}$ in direzione della regione che contiene la nornale a $d\overrightarrow{𝒮}$. Questo è il caso in cui la componente $\overrightarrow{𝒜}\cdot \overrightarrow{𝓃}$ è positiva. Con questa interpretazione, l'integrale di superficie $\underset{S}{\iint }\overrightarrow{𝒜}\cdot dSo\underset{S}{\iint }\overrightarrow{𝒜}\cdot \overrightarrow{𝓃}dS$ è denominato flusso uscente del vettore $d\overrightarrow{𝒜}$ dalla superficie S. Dato che $\overrightarrow{𝒜}\cdot \overrightarrow{𝓃}$ puo essere positiva in taluni punti e negativa in altri della superficie S, con flusso uscente di $d\overrightarrow{𝒜}$ dalla superficie S intendiamo di fatto il flusso netto uscente di $\overrightarrow{𝒜}$.
L' integrali$\underset{S.c}{\iint }\overrightarrow{𝒜}\cdot d\overrightarrow{𝒮}o\underset{S.c}{\iint }\overrightarrow{𝒜}\cdot \overrightarrow{𝓃}dS$ è il flusso di $\overrightarrow{𝒜}$ attraverso la superficie S della regione delimitata da S.

superficie chiusa

Integrale di volume

Consideriamo una regione di spazio R nel campo di una funzione scalare di posizione $\varphi (\overrightarrow{𝓇})$. Poniamo che la regione sia divisa in un numero di elementi volumetrici infinitesimali $d\tau$. Allora l'integrale

$\underset{s}{\iiint }\varphi (\overrightarrow{𝓇})d\tau$

assunto in ogni parte del volume, è noto come integrale volumetrico di $\varphi$ nella regione R. Il risultato dell'integrale è uno scalare.

Analogamente, se R è una regione dello spazio nel campo di una funzione vettoriale di posizione $\varphi (\overrightarrow{𝓇})$, l'integrale
$\underset{s}{\iiint }\overrightarrow{𝒜}(\overrightarrow{𝓇})d\tau$

è noto come integrale volumetrico di $\overrightarrow{𝒜}$ nella regione R. Il risultato di un tale integrale è un vettore. Template:Avanzamento