Algebra vettoriale/Notazione tensoriale cartesiana

Template:Algebra vettoriale Nella analisi di tanti problemi fisici, assai uso si fa delle coordinate Cartesiane. Le equazioni che governano un problema e le manipolazioni susseguenti vengono elaboraste nella forma di componenti Cartesiane. Una tale forma è abitualmente complessa, qualora ciascun termine debba essere esplicitamente scritto e conseguentemente comporta il danno di occultare la semplicità strutturale delle equazioni, delle manipolazioni e dei risultati. Per sormontare ciò, è sta introdotta una notazione abbreviata fondata su poche semplici convenzioni. Tale notazione è nota come notazione indicizzata di Cartesio. In questo capitolo descriviamo tale notazione, ed esprimiamo nei suoi termini le varie relazioni dell'algebra vettoriale e calcolo. La notazione indicizzata, con indici che appaiono come apici e pedici sui termini considerati, è essenziale nello studio dei tensori. Pertanto tale notazione è nota anche come notazione indicizzata tensoriale cartesiana. L'impiego della notazione indicizzata che presentiamo qui non richiede una conoscenza dei tensori e della analisi tensoriale. La presente notazione è semplicemente una maniera conveniente di operare in forma compatta in termini di coordinate Cartesiane. In ogni modo, la medesima notazione viene usata nello studio dei tensori Cartesiani. Quindi la notazione indicizzata presente è pure nota come notazione tensoriale Cartesiana.

Notazioni per le coordinate cartesiane e per le componenti vettoriali.

Si utilizza un sistema di coordinate Cartesiane destrorso. Indichiamo gli assi con X₁, X₂, X₃, le coordinate con x₁, x₂, x₃ ed i versori di riferimento con $\vec{ℯ_{1}}, \vec{ℯ_{2}}, \vec{ℯ_{3}}$ . Pertanto, in combinazione lineare, il vettore posizione $\vec{𝓇}$ viene espresso con

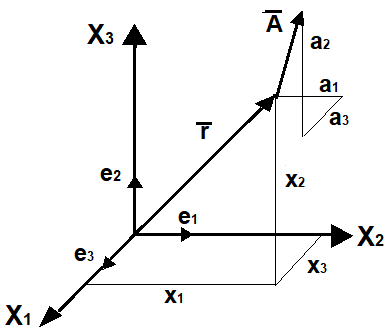
$\vec{𝓇} = x_{1} \vec{ℯ_{1}} + x_{2} \vec{ℯ_{2}} + x_{3} \vec{ℯ_{3}} = \sum_{k = 1}^{3} x_{i} \vec{ℯ_{𝒾}} (1 a)$

Diciamo, in modo equivalente, che $\vec{𝓇}$ è specificato con un insieme di numeri (x₁, x₂, x₃) e scriviamo in maniera simbolica

$\vec{𝓇} : (x_{1}, x_{2}, x_{3}) (1 b)$

per significare che $x_{1}, x_{2}, x_{3}$ sono le componenti di $\vec{𝓇}$ .
Ugualmente, se $a_{1}, a_{2}, a_{3}$ sono le componenti di un vettore $\vec{𝒜}$ , abbiamo
$\vec{𝒜} = a_{1} \vec{ℯ_{1}} + a_{2} \vec{ℯ_{2}} + a_{3} \vec{ℯ_{3}} = \sum_{k = 1}^{3} a_{i} \vec{ℯ_{𝒾}} (2 a)$
o, parimenti,
$\vec{𝒜} : (a_{1}, a_{2}, a_{3}) (2 b)$
E' possibile abbreviare le espressioni (1) e (2) introducendo la notazione che $x_{i}$ indica un insieme di numeri $(x_{1}, x_{2}, z_{3})$ in cui l'indice i assume i valori 1,2,3, e che $a_{i}$ similmente denota di fatto l'insieme di numeri $(a_{1}, a_{2}, a_{3})$ . Con una tale notazione rappresentiamo il vettore $\vec{𝓇}$ con $x_{i}$ ed il vettore $\vec{𝒜}$ con $a_{i}$ ; in modo simbolico scriviamo

$\vec{𝓇} : x_{i} \vec{𝒜} : a_{i}$
Quindi, con questa notazione, un vettore è denotato da un termine con un singolo indice, usato qui come pedice. Per converso, un termine con un singolo indice come, diciamo, $b_{k}$ , deve essere inteso che rappresenti un vettore le cui componenti cartesiane sono $b_{1}, b_{2}, b_{3}$ . E' irrilevante quale nome (o carattere) venga dato all'indice: un termine come $a_{i} o a_{k} o a_{α}$ rappresenterà sempre un vettore le cui componenti sono $a_{1}, a_{2}, a_{3}$ .
A questa notazione ci si riferisce come ad una notazione indicizzata o tensoriale cartesiana, dal momento che ci occupiamo esclusivamente di un sistema di coordinate cartesiane.
Uno scalare, come al solito, verrà indicato con un termine senza indice.

Operazioni algebriche elementari

Per illustrare subito l'uso della notazione con gli indici e la semplicità apportata dalla sua utilizzazione, consideriamo alcune semplici operazioni algebriche.
Nella forma di combinazione lineare l'uguaglianza di due vettori $\vec{𝒜}$ e $\vec{ℬ}$ viene espressa da
$a_{1} \vec{ℯ_{1}} + a_{2} \vec{ℯ_{2}} + a_{3} \vec{ℯ_{3}} = b_{1} \vec{ℯ_{1}} + b_{2} \vec{ℯ_{2}} + b_{3} \vec{ℯ_{3}} (1)$
oppure dalle tre equazioni scalari
$a_{1} = b_{1} a_{2} = b_{2} a_{3} = b_{3} (2)$
Facendo uso della notazione ad indici, le espressioni (1) e (2) possono venire espresse in modo compatto scrivendo
$a_{i} = b_{i}$
Questa equazione sottintende di fatto tre di tali equazioni. cioè, il sistema che si ottiene dando agli indici i valori 1,2,3 (eq.2)
In forma di combinazione lineare la somma di due vettori è espressa da
$\vec{𝒜} + \vec{ℬ} = (a_{1} + b_{1}) \vec{ℯ_{1}} + (a_{2} + b_{2}) \vec{ℯ_{2}} + (a_{3} + b_{3}) \vec{ℯ_{3}} = \sum_{k = 1}^{3} (a_{i} + b_{i}) \vec{ℯ_{𝒾}}$
Nella notazione con indici la somma è espressa semplicemente da
$a_{i} = b_{i} (3)$
che significa un vettore le cui componenti sono date dalla espressione (3) quando ad i siano dati i valori 1,2,3.
Per concludere, consideriamo un vettore $\vec{𝒸}$ dato da
$\vec{𝒸} = m \vec{𝒜}$
in cui m è uno scalare. Nel formato di combinazione lineare si ha
$c_{1} \vec{ℯ_{1}} + c_{2} \vec{ℯ_{2}} + c_{3} \vec{ℯ_{3}} = m (a_{1} \vec{ℯ_{1}} + a_{2} \vec{ℯ_{2}} + a_{3} \vec{ℯ_{3}})$
o, in modo equivalente, le tre equazioni scalari
$c_{1} = m a_{1} c_{2} = m a_{2} c_{3} = m a_{3}$
Usando la notazione ad indici, il contenuto di () e () viene espresso in modo compatto da
$c_{i} = m a_{i}$
Ripetiamo che una notazione come () significa uguaglianza di due vettori, una espressione quale () significa addizione di due vettori, ed un termine come ma_i sottintende la moltiplicazione di un vettore per uno scalare.

Template:Avanzamento

prodotto scalare

Nella forma componenti il prodotto scalare è espresso da
$\vec{𝒜} \cdot \vec{ℬ} = a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}$
Ricorrendo alla notazione ad indici, ciò può essere riscritto come
$\vec{𝒜} \cdot \vec{ℬ} = \sum_{k = 1}^{3} a_{i} b_{i}$
Parimenti, si ha
$\vec{𝒜} \cdot \vec{𝒜} = \sum_{k = 1}^{3} a_{i} a_{i}$

convenzione della sommatoria

Il lato destro di $\vec{𝒜} \cdot \vec{ℬ} = \sum_{k = 1}^{3} a_{i} b_{i}$ , come quello di $\vec{𝒜} \cdot \vec{𝒜} = \sum_{k = 1}^{3} a_{i} a_{i}$ , è la somma di tre termini ottenuti dando a turno, alla i i valori 1,2,3,e procedendo alla somma . Notiamo che l'indice nel termine generico della somma viene ripetuto come nel caso di i in $a_{1} b_{1}$ . La somma, diciamo, è su un indice ripetuto.Essendo questo il caso, una semplificazione viene raggiunta se sopprimiamo il simbolo $Σ$ della sommatoria e lo sostituiamo con la convenzione che quando un indice è ripetuto in un termine un tale termine è da sommare a tutti i valori di tale indice. In molte situazioni, come si vedrà, la sommatoria si verifica sempre su un indice ripetuto. Questa convenzione è nota come convenzione della sommatoria. Essa venne introdotta da Einstein e viene indicata pure come convenzione della sommatoria di Einstein.
Con questa convenzione i prodotti scalari $\vec{𝒜} \cdot \vec{ℬ} = \sum_{k = 1}^{3} a_{i} b_{i}$ e $\vec{𝒜} \cdot \vec{𝒜} = \sum_{k = 1}^{3} a_{i} a_{i}$ possono venire espressi in forma compatta
$\vec{𝒜} \cdot \vec{ℬ} = a_{i} b_{i} \vec{𝒜} \cdot \vec{𝒜} = a_{i} a_{i}$

A proposito, le quazioni
$\vec{𝓇} = x_{1} \vec{ℯ_{1}} + x_{2} \vec{ℯ_{2}} + x_{3} \vec{ℯ_{3}} = \sum_{k = 1}^{3} x_{i} \vec{ℯ_{𝒾}}$
$\vec{𝒜} = a_{1} \vec{ℯ_{1}} + a_{2} \vec{ℯ_{2}} + a_{3} \vec{ℯ_{3}} = \sum_{k = 1}^{3} a_{i} \vec{ℯ_{𝒾}}$
$\vec{𝒜} + \vec{ℬ} = (a_{1} + b_{1}) \vec{ℯ_{1}} + (a_{2} + b_{2}) \vec{ℯ_{2}} + (a_{3} + b_{3}) \vec{ℯ_{3}} = \sum_{k = 1}^{3} (a_{i} + b_{i}) \vec{ℯ_{𝒾}}$
possono ora venire scritte come
$\vec{𝓇} = x_{i} \vec{ℯ_{𝒾}}$
$\vec{𝒜} = a_{i} \vec{ℯ_{𝒾}}$
$\vec{𝒜} + \vec{ℬ} = (a_{i} + b_{i}) \vec{ℯ_{𝒾}}$ .

Template:Avanzamento

Algebra vettoriale/Notazione tensoriale cartesiana

Indice

Notazioni per le coordinate cartesiane e per le componenti vettoriali.

Operazioni algebriche elementari

prodotto scalare

convenzione della sommatoria

Menu di navigazione

Algebra vettoriale/Notazione tensoriale cartesiana

Notazioni per le coordinate cartesiane e per le componenti vettoriali.

Operazioni algebriche elementari

prodotto scalare

convenzione della sommatoria

Menu di navigazione

Ricerca