Analisi matematica I/Funzioni circolari

Circonferenza unitaria

La circonferenza unitaria , detta anche goniometrica è la circonferenza con centro nell'origine e raggio 1.

Per brevità la indicheremo con $U=\{z\in ℂ:|u|=1\}$ la circonferenza unitaria e con $U^{+}$ la semicirconferenza unitaria formata dai complessi con parte immaginaria non negativa, cioè in altri termini primo e quatro quadrante.
Definiamo poi l' arco di estremi 1 e $v$ l'insieme dei punti di $U^{+}$ tali che la parte reale di ogni punto di questo insieme sia minore uguale di $v$.

Notiamo che per ogni punto di $U$ esiste un solo $\alpha \in U^{+}$ tale che ${\alpha }^2=u$. Infatti se così non fosse, avremmo che $u^2-{\alpha }^2=0$ e di conseguenza $(u-\alpha )(u+\alpha )=0$, che implica $u=\alpha$ o $u=-\alpha$. Ma per ipotesi $\alpha \in U^{+}$ e dunque non è possibile che anche $-\alpha \in U^{+}$ e dunque non può essere $u=-\alpha$ e così l'unicità è dimostrata.
Ponendo (sempre considerandoci in $U^{+}$

$\alpha =\frac{1+u}{|1+u|}$

si ha infatti:

${\left(\frac{1+u}{|1+u|}\right)}^2=\frac{{(1+2u+u^2)}^2}{{\left(\sqrt{{\mathrm{\Re }}^2(1+u)+{\mathrm{\Im }}^2(1+u)}\right)}^2}=\frac{1+2(a+ib)+a^2+2aib-b^2}{{\left(\sqrt{(1+a{)}^2+b^2}\right)}^2}$. Ora, ricordando che $a^2+b^2=1$ perché ${\cos }^{2}x+{\sin }^{2}x=1$ e sostituendo al numeratore $b^2$ con $a^2-1$, abbiamo

$=\frac{2a+2a^2+2ib(a+1)}{2+2a}=\frac{(a+1)(a+ib)}{a+1}=a+ib=u$.

Graficamente, $\alpha$ è il punto medio dell'arco da $1$ ad $u$.

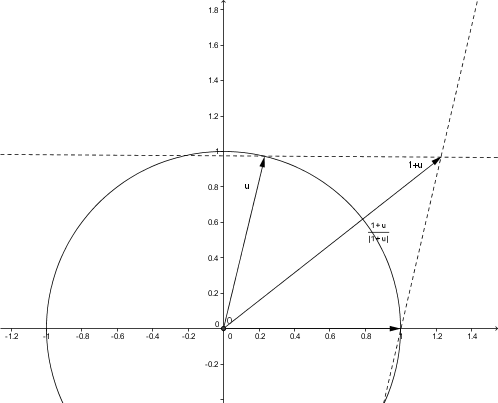
Definiamo poi una successione $\alpha (u):\mathbb{N}\to ℂ$ tale che

$\{\begin{array}{c}{\alpha }_0(u)=u\\ {\alpha }_{n+1}(u)=\alpha (\alpha (n))\end{array}$.

In altri termini, abbiamo definito la successione "punto medio" di ogni segmento tale da creare segmenti sempre più piccoli avvicinandosi sempre di più alla circonferenza, per $n$ che tende all'infinito.

Definiamo un'altra successione estremamente importante: la successione "lunghezza dell'arco" da $1$ a $u$ come

$L_n:\mathbb{N}\to ℂ$

$L_n(u)=2^n|\alpha (n)-1|$

cioè, la lunghezza dell'arco trovato per ogni $n\in \mathbb{N}$ applicato alla successione $\alpha$ comporta che il segmento disti $|\alpha (n)-1|$ e dunque, siccome sono $2^n$, la lunghezza dell'intero arco fino ad $u$ è data da $2^n|\alpha (n)-1|$. La figura sotto chiarisce meglio la situazione ad esempio, nel caso di $n=2$.

Poniamo infine $\pi :=L(-1)$ (in accordo con l'usuale conoscenza che abbiamo di $\pi$ come $180^{\circ }$.

Osservazioni sulla funzione lunghezza dell'arco

Vediamo ora alcuni aspetti importanti di $L(u)$ e di $\alpha (u)$.
Siano $u\in U^{+}$ e $v\in U\setminus \{0\}$. Si ha allora che

$\alpha (uv)=\alpha (u)\alpha (v)$.

Per definizione di $\alpha (u)$ sappiamo che è quell'unico elemento tale che ${\alpha }^2(u)=u$. Notiamo però che $(\alpha (u)\alpha (v){)}^2=uv$ e dunque è quell'unico elemento in $U^{+}$ che elevato al quadrato da $uv$. Quindi è $\alpha (uv)$.

Inoltre, $L(uv)=L(u)+L(v)$. La dimostrazione la omettiamo per brevità, ma vi invitiamo a darci un'occhiata sul libro di testo che avete. Osserviamo solo che

$L(u)=\pi +L(-u),\mathrm{\forall }u\in U\setminus U^{+}$

Infatti, nel caso $u\ne -1$, visto che $u\in U\setminus U^{+}$, $-u\in U^{+}$ e dunque

$L(u)=L((-1)(-u))=L(-1)+L(-u)=\pi +L(-u)$.

Proposizione (biiettività della funzione lunghezza dell'arco)

Template:Riquadro Non dimostreremo questa proposizione adesso in quanto si richiedono conoscenze di continuità e di connessione che vedremo più avanti. Per ora, accettate "con fiducia" quanto detto.

Per ogni $t\in [0,2\pi [$ poniamo

$e^{it}=L^{-1}(t),\mathrm{\forall }t\in [0,2\pi [$

$e^{i(t-2k\pi )}=L^{-1}(t-2k\pi ),\mathrm{\forall }t\in ℝ$

.

Essendo $e^{it}\in U$, possiamo porre

$\cos t=\mathrm{\Re }{e}^{it}\sin t=\mathrm{\Im }{e}^{it}$