Elaborazione numerica dei segnali/DFT e FFT

Trasformata di Fourier discreta (DFT)

Definizione di DFT

Data una sequenza $x\left(n\right)$ costituita da un numero $N$ finito di campioni, la sua trasformata di Fourier discreta (Template:Tooltip) $X\left(k\right)$, all'interno del suo periodo $N$, è definita:

$X\left(k\right)=\sum _{n=0}^{N-1}x\left(n\right)e^{-j2\pi n\frac{k}{N}},k=0,1,2,\dots ,N-1$

e può essere interpretata come la discretizzazione in frequenza della DTFT $X\left(e^{j2\pi f}\right)$, di cui vengono prese $N$ frequenze $f_k$ equispaziate:

$f_k=\frac{k}{N},k=0,1,2,\dots ,N-1$

Dal punto di vista algoritmico, la DFT è di complessità inferiore rispetto alla DTFT, e inoltre è definita in modo discreto → è rappresentabile su un calcolatore.

Inversione della DFT (IDFT)

L'antitrasformata della DFT, all'interno del suo periodo $N$, è definita:

$x\left(n\right)=\frac{1}{N}\sum _{k=0}^{N-1}X\left(k\right)e^{j2\pi n\frac{k}{N}},n=0,1,2,\dots ,N-1$

Estensioni periodiche

La DFT e la IDFT sono periodiche di periodo $N$:

$\{\begin{array}{c}X\left(k\right)=X(k+N)k=0,\dots ,N-1\\ x\left(n\right)=x(n+N)n=0,\dots ,N-1\end{array}$

Si definiscono le estensioni periodiche $\bar{X}\left(k\right)$ e $\bar{x}\left(n\right)$, rispettivamente di $X\left(k\right)$ e $x\left(n\right)$:

$\{\begin{array}{c}\bar{X}\left(k\right)=\sum _{n=0}^{N-1}x\left(n\right)e^{-j2\pi n\frac{k}{N}}\mathrm{\forall }k\\ \bar{x}\left(n\right)=\frac{1}{N}\sum _{k=0}^{N-1}X\left(k\right)e^{j2\pi n\frac{k}{N}}\mathrm{\forall }n\end{array}$

Tecnica di aggiunta degli zeri

È possibile teoricamente ricavare per interpolazione la DTFT partendo dagli $N$ campioni della DFT:

$X\left(e^{j2\pi f}\right)=\frac{1}{N}\sum _{k=0}^{N-1}X\left(k\right)\frac{\sin (\pi Nf-k\pi )}{\sin (\pi f-\pi \frac{k}{N})}{e}^{-j\pi (N-1)(f-\frac{k}{N})}$

In pratica la DTFT viene approssimata a una DFT definita su un nuovo periodo $N_1\gg N$, applicata a una sequenza $x_z\left(n\right)$ che non è altro che la sequenza di partenza $x\left(n\right)$ a cui sono stati accodati $N_1-N$ campioni nulli:

$x_z\left(n\right)=\{\begin{array}{cc}x\left(n\right)& n=0,\dots ,N-1\\ 0& n=N,\dots ,N_1-1\end{array}$

Aggiungere degli zeri in fondo alla sequenza $x\left(n\right)$ permette di aumentare artificialmente il periodo della sua DFT senza alterare la DTFT a cui si cerca di approssimare:

$X\left(e^{j2\pi f_k}\right)=\sum _{n=0}^{N-1}x\left(n\right)e^{-j2\pi f_{k}n}=\sum _{n=0}^{N_1-1}{x}_z\left(n\right)e^{-j2\pi \frac{k}{N_1}n}k=0,\dots ,N_1-1$

e siccome il numero di campioni presi dalla DTFT è maggiore, la risoluzione della DTFT risulta molto più alta.

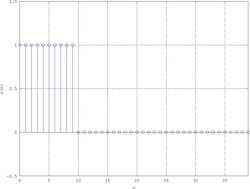
Esempio - Sequenza porta

$x\left(n\right)=\{\begin{array}{cc}1& 0\le n\le N-1\\ 0& n\ge N\end{array}$

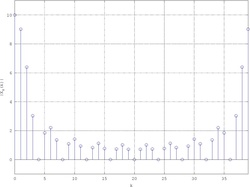
Considerando solamente l'intervallo $[0,N-1]$ si ottiene come DFT $\left|X\left(k\right)\right|$ una funzione $\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}$ campionata a una frequenza molto bassa:

$X\left(k\right)=\sum _{n=0}^{N-1}x\left(n\right)e^{-j2\pi n\frac{k}{N}}=\sum _{n=0}^{N-1}{e}^{-j2\pi n\frac{k}{N}}=\frac{1-e^{-j2\pi k}}{1-e^{-j2\pi \frac{k}{N}}}=\{\begin{array}{cc}0& k\ne 0\\ N& k=0\end{array}$

$N_1=N$

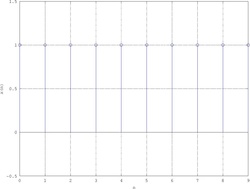
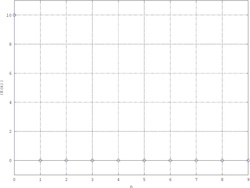
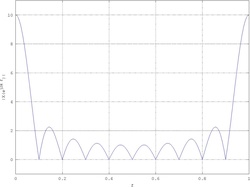
Basta però aggiungere degli zeri a destra della porta per migliorare la risoluzione della DTFT:

$N_1=2N$

---

$N_1=4N$

---

$N_1=100N$

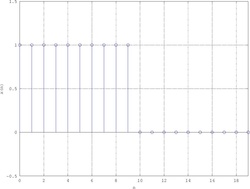
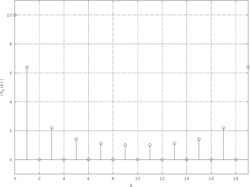
Aliasing nel tempo

Partendo dalla sequenza $x\left(n\right)$ di durata non finita:

$x\left(n\right)=a^{n}u\left(n\right)0<a<1$

la sua DTFT campionata nel primo periodo $N$:

$X\left(k\right)=X\left(e^{j2\pi \frac{k}{N}}\right)=\frac{1}{1-a^{-j2\pi \frac{k}{N}}}k=0,\dots ,N-1$

non coincide esattamente con la DFT calcolata sulla sequenza troncata:

$X_N\left(k\right)=\frac{1-a^N}{1-a^{-j2\pi \frac{k}{N}}}k=0,\dots ,N-1$

perché vi è un effetto di aliasing nel tempo dovuto al fatto che la sequenza $x\left(n\right)$ di partenza non ha durata finita.

Al crescere dell'ampiezza del periodo $N$, la DFT della sequenza troncata tende sempre di più alla DTFT campionata nel primo periodo.

Proprietà della DFT

Accorgimenti

Le proprietà della DFT sono analoghe a quelle della DTFT, ma ci vogliono alcuni accorgimenti:

• la DFT $X\left(k\right)$ è periodica di periodo $N$ → le operazioni sulla DFT $X\left(k\right)$ devono condurre a una sequenza periodica di periodo $N$;
• la IDFT $x\left(n\right)$ è periodica di periodo $N$ → le operazioni sulla IDFT $x\left(n\right)$ devono condurre a una sequenza periodica di periodo $N$.

Operatore di modulo

L'operatore di modulo restituisce sempre un numero compreso in $[0,N-1]$:

${\left|k\right|}_N=k\text{ mod }N$

Se $k$ è un numero negativo, si somma $N$ a $k$ tante volte fino a ottenere un numero compreso in $[0,N-1]$:

${|-13|}_{16}=3$

Operatore di ritardo circolare

L'operatore di ritardo circolare restituisce una sequenza ritardata che è ancora compresa in $[0,N-1]$:

$x\left({|n-N_0|}_k\right)$

in quanto i campioni che vanno al di là del primo periodo ricompaiono all'inizio del primo periodo stesso.

Modo operativo

• si genera la sequenza periodicizzata $\bar{x}\left(n\right)$;
• si applica il ritardo di $N_0$ campioni a $\bar{x}\left(n\right)$: $\bar{x}(n-N_0)$;
• la sequenza ritardata $x(n-N_0)$ è pari alla sequenza periodicizzata $\bar{x}(n-N_0)$ troncata nel primo periodo $N$ ($n\in [0,N-1]$).

Convoluzione circolare

La convoluzione circolare tra due sequenze $x\left(n\right)$ e $y\left(n\right)$ è definita:

$x\left(n\right)\otimes y\left(n\right)=\sum _{k=0}^{N-1}x\left(k\right)y\left({|n-k|}_N\right)$

dove $N$ è la più grande tra le durate delle singole sequenze.

Proprietà commutativa

$x\left(n\right)\otimes y\left(n\right)=y\left(n\right)\otimes x\left(n\right)$

La convoluzione circolare si può rappresentare con un prodotto matrice per vettore. Ad esempio, se la durata $N$ è pari a 4:

$x\left(n\right)\otimes y\left(n\right)=\left[\begin{array}{cccc}y\left(0\right)& y\left(3\right)& y\left(2\right)& y\left(1\right)\\ y\left(1\right)& y\left(0\right)& y\left(3\right)& y\left(2\right)\\ y\left(2\right)& y\left(1\right)& y\left(0\right)& y\left(3\right)\\ y\left(3\right)& y\left(2\right)& y\left(1\right)& y\left(0\right)\end{array}\right]\left[\begin{array}{c}x\left(0\right)\\ x\left(1\right)\\ x\left(2\right)\\ x\left(3\right)\end{array}\right]$

Linearità

$z\left(n\right)=a_{1}x\left(n\right)+a_{2}y\left(n\right)\Rightarrow Z\left(k\right)=a_{1}X\left(k\right)+a_{2}Y\left(k\right)$

Ritardo

$z\left(n\right)=x\left({|n-N_0|}_N\right)\Rightarrow Z\left(k\right)=X\left(k\right)e^{-j2\pi \frac{k}{N}{N}_0}$

Modulazione

$z\left(n\right)=e^{j2\pi \frac{k_0}{N}n}x\left(n\right)\Rightarrow Z\left(k\right)=X\left({|k-k_0|}_N\right)$

Convoluzione circolare

$z\left(n\right)=x\left(n\right)\otimes y\left(n\right)\Rightarrow Z\left(k\right)=X\left(k\right)\cdot Y\left(k\right)$

Accorgimenti

• la convoluzione circolare di due sequenze di durata $N$ campioni ha una uguale durata di $N$ campioni (a differenza della convoluzione lineare della DTFT, la cui sequenza risultante ha durata $2N-1$ campioni);
• la convoluzione circolare $\bar{z}\left(k\right)$ di due IDFT $\bar{x}\left(k\right)$ e $\bar{y}\left(k\right)$, entrambe di periodo $N$, è periodica di periodo $N$:

  $\bar{z}(n+N)=\sum _{k=0}^{N-1}\bar{x}\left(k\right)\bar{y}(n+N-k)=\sum _{k=0}^{N-1}\bar{x}\left(k\right)\bar{y}(n-k)=\bar{z}\left(n\right)$

Proprietà di simmetria

Se la sequenza $x\left(n\right)$ è reale:

• $X\left(k\right)=X_R\left(k\right)+j{X}_I\left(k\right)$
  • se $x\left(n\right)$ è una sequenza pari: $X_I\left(k\right)=0$;
  • se $x\left(n\right)$ è una sequenza dispari: $X_R\left(k\right)=0$;
• per la DFT vale la simmetria hermitiana intorno a 0:

  $X\left(k\right)=X^{*}\left({|-k|}_N\right)$

• per la DFT vale la simmetria hermitiana intorno a $\frac{N}{2}$;
• il campione in $k=0$ della DFT è sempre reale:

  $X^{*}\left(0\right)=X\left(0\right)=\sum _{n=0}^{N-1}x\left(n\right)$

Trasformata di Fourier veloce (FFT)

La DFT ha complessità quadratica ($N^2$).

La Template:Tooltip è un algoritmo di complessità linearitmica ($N\log N$) che implementa la DFT e la IDFT in maniera più efficiente.

DFT

La DFT può essere rappresentata in termini di matrici:

$𝐗=𝐇𝐱;\left[\begin{array}{c}X\left(0\right)\\ X\left(1\right)\\ X\left(2\right)\\ ⋮\\ X(N-1)\end{array}\right]=\left[\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& H_N^1& H_N^2& \cdots & H_N^{N-1}\\ 1& H_N^2& H_N^4& \cdots & H_N^{2(N-1)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& H_N^{N-1}& H_N^{2(N-1)}& \cdots & H_N^{(N-1)(N-1)}\end{array}\right]\cdot \left[\begin{array}{c}x\left(0\right)\\ x\left(1\right)\\ x\left(2\right)\\ ⋮\\ x(N-1)\end{array}\right]$

dove:

$H_N=e^{-j2\pi \frac{1}{N}}\Rightarrow H_N^{nk}=e^{-j2\pi n\frac{k}{N}}$

Algoritmo della decimazione nel tempo

L'algoritmo della decimazione nel tempo è un algoritmo di tipo "divide et impera" che riduce la complessità dell'algoritmo di DFT.

Ipotesi

$N$ è una potenza di 2

Divide

La sequenza si suddivide in due sottosequenze costituite da metà campioni:

• la sottosequenza $x_0\left(n\right)$ è formata dai campioni pari:

  $x_0\left(n\right)=x\left(2n\right)n=0,\dots ,\frac{N}{2}-1$

• la sottosequenza $x_1\left(n\right)$ è formata dai campioni dispari:

  $x_1\left(n\right)=x(2n+1)n=0,\dots ,\frac{N}{2}-1$

Ricombinazione

Ogni DFT $X\left(k\right)$, elemento del vettore $𝐱$, si ottiene dalla somma delle DFT delle singole sottosequenze $x_0\left(n\right)$ e $x_1\left(n\right)$:

$X\left(k\right)=X_0\left({\left|k\right|}_{\frac{N}{2}}\right)+H_N^k{X}_1\left({\left|k\right|}_{\frac{N}{2}}\right)=\sum _{n=0}^{\frac{N}{2}-1}{x}_0\left(n\right)H_{\frac{N}{2}}^{nk}+H_N^k\sum _{n=0}^{\frac{N}{2}-1}{x}_1\left(n\right)H_{\frac{N}{2}}^{nk}$

Complessità

Il numero totale di operazioni (somme e prodotti) complesse è pari a:

$N+\frac{N^2}{2}<N^2$

Si può quindi riapplicare ripetutamente il procedimento "divide et impera" sulle sottosequenze. Al passo $k$-esimo si ha una complessità pari a:

$k\cdot N+2^k{\left(\frac{N}{2^k}\right)}^{2}k=1,\dots ,{\log }_{2}N$

All'ultimo passo ($k={\log }_{2}N$), quando si arriva a dover valutare le DFT su 1 punto, la complessità totale è linearitmica:

${\log }_{2}N\cdot N+N\approx {\log }_{2}N\cdot N$

Riduzione di complessità

La complessità può essere ulteriormente ridotta sfruttando le proprietà di simmetria della matrice $𝐇$.

Esempio con $N=4$ campioni

$\{\begin{array}{c}X\left(0\right)=x\left(0\right)+x\left(2\right)+x\left(1\right)+x\left(3\right)\\ X\left(1\right)=x\left(0\right)+H_{2}x\left(2\right)+H_4[x\left(1\right)+H_{2}x\left(3\right)]\\ X\left(2\right)=x\left(0\right)+x\left(2\right)+H_4^2[x\left(1\right)+x\left(3\right)]\\ X\left(3\right)=x\left(0\right)+H_{2}x\left(2\right)+H_4^3[x\left(1\right)+H_{2}x\left(3\right)]\end{array}$

Schema circuitale a farfalla

IDFT

Tutte le considerazioni sulla DFT valgono anche per la IDFT: basta applicare l'algoritmo sul complesso coniugato della DFT e poi dividere per $N$:

$x\left(n\right)=\frac{1}{N}\sum _{k=0}^{N-1}X\left(k\right)e^{j2\pi n\frac{k}{N}}=\frac{1}{N}{\left[\sum _{k=0}^{N-1}{X}^{*}\left(k\right)e^{-j2\pi n\frac{k}{N}}\right]}^{*}\Rightarrow x\left(n\right)=\text{IDFT}\left[X\left(k\right)\right]=\frac{1}{N}\text{DFT}\left[X^{*}\left(k\right)\right],n=0,1,2,\dots ,N-1$