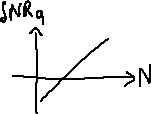Elettronica applicata/Sistemi di conversione A/D e D/A

Schema a blocchi di un sistema di conversione A/D/A

Un segnale analogico è più facile da elaborare se viene campionato in un segnale numerico, cioè a tempo discreto (campionamento) e discreto in ampiezza (quantizzazione). Template:Clear

Campionamento

Il campionamento consiste nella moltiplicazione del segnale analogico $x\left(t\right)$ per un treno di impulsi (delta):

• 
  Campionamento nel dominio del tempo
• 
  Campionamento nel dominio della frequenza

• nel dominio del tempo si ottiene una sequenza equispaziata di suoi campioni:

  $x_S\left(t\right)=x\left(t\right)\sum _{n=-\mathrm{\infty }}^{+\mathrm{\infty }}\delta (t-n{T}_S)$

• nel dominio della frequenza si ottiene una trasformata periodica di periodo $\frac{2\pi }{T_S}$:

  $X_S\left(\omega \right)=\frac{1}{T_S}\sum _{n=-\mathrm{\infty }}^{+\mathrm{\infty }}X(\omega -n\frac{2\pi }{T_S})$

Teorema del campionamento

Ricostruzione del segnale in assenza di aliasing

Aliasing

Per ricostruire il segnale campionato serve un filtro passa-basso che elimini le repliche dello spettro periodico lasciando solo quella centrata intorno all'origine.

Un segnale a tempo continuo può essere campionato e perfettamente ricostruito a partire dai suoi campioni se la frequenza di campionamento $F_S$ è maggiore del doppio della banda $F_M$ del segnale:

$F_S\triangleq \frac{1}{T_S}>2F_M$

Il teorema del campionamento (o di Nyquist) garantisce l'assenza di aliasing, ovvero evita che le repliche in frequenza si sovrappongano e quindi il filtro passa-basso non riesca più a isolare lo spettro principale.

Filtro anti-aliasing

La maggioranza dei segnali utilizzati nella realtà ha banda illimitata: esiste un intervallo al di fuori del quale il segnale è significativamente vicino a zero, ma non è mai identicamente nullo. Il segnale campionato quindi presenterà nel dominio della frequenza delle sovrapposizioni degli spettri (rumore di campionamento) che alla fine non possono essere ricostruite dal filtro passa-basso. Il filtro anti-aliasing serve per eliminare le parti ad alta frequenza prima del campionamento. Template:Vedi anche Template:Clear

Sample e hold

Segnale campionato e mantenuto

Filtro di ricostruzione

Un circuito logico non può lavorare su campioni dalla durata infinitesima (delta) → un modulo di sample e hold legge il valore del segnale a tempi prefissati e quindi mantiene stabile tale valore fino al campione successivo.

Il mantenimento ha l'effetto di attenuare le componenti spettrali ad alta frequenza → il filtro di ricostruzione deve tener conto della distorsione spettrale dovuta al mantenimento tramite un peaking verso il limite di banda. Template:Vedi anche Template:Clear

Quantizzazione

Quantizzazione

Rappresentazione xy

Errore di quantizzazione

L'operazione di quantizzazione permette di rappresentare un segnale in forma numerica: ogni campione del segnale campionato viene approssimato al livello associato all'intervallo a cui appartiene. L'intervallo di ampiezze $S$ è suddiviso in un numero finito $2^N$ intervalli di ampiezza uniforme; al centro di ogni intervallo vi è un livello, che è rappresentato da una sequenza di $N$ bit.

Si definisce errore (o rumore) di quantizzazione ${\epsilon }_q$ la differenza fra un campione reale e la sua versione quantizzata:

$\left|{\epsilon }_q\right|\le \frac{S}{2^{N+1}}$

La qualità del segnale quantizzato è espressa in termini del rapporto segnale/rumore ${\text{SNR}}_q$:

${\text{SNR}}_q=\frac{{\sigma }_A^2}{{\sigma }_{{\epsilon }_q}^2}$

dove:

• ${\sigma }_A^2$ è la potenza del segnale non ancora quantizzato;
• ${\sigma }_{{\epsilon }_q}^2$ è la potenza del rumore di quantizzazione ${\epsilon }_q$:

  ${\sigma }_{{\epsilon }_q}^2=\frac{S^2}{12\cdot 4^N}$

A parità di ampiezza $S$, il rapporto segnale/rumore:

• 
  ${\text{SNR}}_q$ al variare di $N$
• 
  ${\text{SNR}}_q$ al variare di $A$

• aumenta linearmente all'aumentare del numero di bit;
• aumenta linearmente all'aumentare della dinamica $A$ del segnale, ma diminuisce velocemente se la dinamica del segnale supera l'ampiezza $S$ → serve un modulo amplificatore per far sì che la dinamica massima del segnale sia pari all'ampiezza di fondo scala $S$: D5. Condizionamento del segnale#Amplificatore di condizionamento.