Esercizi di fisica con soluzioni/Il I principio della termodinamica

Esercizi

1. Isobara irreversibile

Alla temperatura $T_0$ e alla pressione $p_0$ una certa quantità di idrogeno (gas biatomico, ideale) occupa un volume $V_0$. Ad un certo istante il gas viene messo a contatto con una sorgente di calore ad una certa temperatura. Se si aspetta un tempo sufficientemente lungo, il volume del gas raddoppia mentre la pressione rimane eguale. Determinare la temperatura finale del gas e la variazione di energia interna del gas.

(dati del problema $T_0=0{}^{o}C$, $p_0=10^{5}Pa$, $V_0=0.0015m^3$)

2. Adiabatica gas perfetto

Una mole di un gas perfetto biatomico si espande adiabaticamente (reversibilmente) fino ad occupare un volume doppio di quello iniziale. Determinare la temperatura finale e il lavoro fatto.

(dati del problema temperatura iniziale $T_1=127{}^{o}C$)

3. Adiabatica con recipiente

$n$ moli di un gas monoatomico ideale sono contenute in un recipiente metallico di capacità molare $3R$ e di numero di moli $\alpha n$. Il gas esegue una trasformazione reversibile adiabatica. Determinare il valore del coefficiente $\gamma$ (equivalente) della trasformazione adiabatica in funzione di $\alpha$.

(dati del problema $\alpha =0.1,1,10$)

4. Ciclo di Stirling

Un ciclo di Stirling consiste di due isoterme a temperatura $T_1$ e $T_2$ e due isocore a volume $V_A$ e l'altra a volume $V_B$. Il ciclo viene eseguito da un gas monoatomico con quindi capacità molare a volume costante pari a $c_v=3/2R$. Immaginando che il ciclo venga percorso per stati di equilibrio termodinamico ed in particolare che le due isoterme siano reversibili.

Determinare il rendimento del ciclo:

a) Nel caso che le isocore siano reversibili.

b) Nel caso che vi siano due sole sorgenti di temperatura.

c) Nel caso vi sia una sorgente di calore a temperatura intermedia tra $T_1$ e $T_2$.

(dati del problema $T_1=310K$, $T_2=500K$, $V_A=0.002m^3$, $V_B=0.004m^3$)

5. Ciclo anomalo

Una mole di un gas ideale monoatomico, alla temperatura $T_A$, occupa inizialmente il volume $V_A$. Al gas viene fatta compiere una trasformazione isobara, per stati di equilibrio termodinamico, che porta il volume in $B$, una trasformazione adiabatica reversibile lo porta in $C$ che ha un volume doppio dello stato iniziale ($V_C=2V_A$). Infine una trasformazione isoterma $C->A$ reversibile riporta il sistema nello stato iniziale.

Determinare:

a) La temperatura in B.

b) Il lavoro fatto globalmente

c) Il rendimento del ciclo.

(dati del problema $T_A=300K$, $V_A=0.001m^3$)

6. Ciclo irreversibile

Una quantità pari a $n=0.3$ moli di gas ideale biatomico sono contenuti in un cilindro dotato di pistone ($c_V=\frac{5}{2}R$ e $R=8.314J/K$). Inizialmente il sistema è in equilibrio (stato A) alla temperatura ambiente $T_A=297K$ e alla pressione $P_A$ determinata dalla pressione ambiente $0.95\times 10^{5}Pa$ e dalla forza peso della massa $M=5.1kg$ del pistone (su area del cilindro $S=0.002m^2$). Con il pistone bloccato il gas viene messo in contatto con una sorgente a temperatura $T_B=500K$ fino ad ottenere l'equilibrio termico (stato B). Il pistone viene quindi sbloccato e il gas subisce (in contatto con la sorgente $T_B$) una espansione irreversibile compiendo lavoro contro la pressione esterna $P_A$ fino a raggiungere un nuovo stato di equilibrio C.

Determinare: a) la pressione del gas nello stato A; b) la pressione del gas in B; c) il calore assorbito durante la trasformazione $A\to B$; d) lo spostamento $h$ del pistone nella trasformazione $B\to C$ ed il lavoro eseguito; e) il rendimento del ciclo se venisse chiuso con una isobara reversibile $C\to A$.

7. Trasformazione politropica

$n=1.2$ moli di un gas ideale monoatomico alla temperatura iniziale $T_o=25{}^{o}C$ eseguono una trasformazione generica reversibile di equazione $T{V}^{-3}=cost$, aumentando del 40% il volume iniziale $V_o$, cioè $V_f=\alpha V_o$ con $\alpha =1.4$. Determinare: a) la temperatura finale del gas; b) il lavoro fatto durante la trasformazione; c) il calore assorbito durante la trasformazione.

8. Molla e pistone

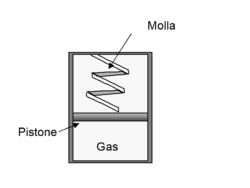
Un gas ideale monoatomico ($n=0.3moli$) è confinato in un recipiente cilindrico con pareti rigide ed isolanti, base conduttrice inizialmente in contatto con una sorgente a temperatura $T_0=300K$, e delimitato da un pistone mobile senza attrito di spessore e massa trascurabile. Inizialmente il gas è in equilibrio termodinamico e il pistone, sul quale agisce la sola forza di compressione di una molla di costante elastica $K=50000N/m$, delimita un volume di altezza $h=20cm$.

Il volume iniziale in cui è contenuto il gas vale $Sh$, ma la sezione $S$ del cilindro non è necessaria conoscerla. A partire dalla configurazione iniziale si fornisce calore al gas (attraverso la base conduttrice) fino a comprimere la molla ad un valore doppio di quello iniziale. Determinare: a) la compressione iniziale $\mathrm{\Delta }l$ della molla; b) la temperatura finale $T_f$ del gas; c) il calore $Q_a$ assorbito dal gas.

9 Ciclo irreversibile con isocora

Un gas monoatomico compie il ciclo termodinamico riportato in figura: dalla temperatura $T_2$ il gas si espande in maniera adiabatica e irreversibile riducendo del 10% il lavoro prodotto nella espansione (ma le relazioni tra P,V,T sono quelle di una adiabatica reversibile) e portandosi alla temperatura ambiente $T_1$ e alla pressione atmosferica $P_B$ con un volume $V_B$. A questo punto una compressione isoterma reversibile alla temperatura $T_1$ riporta il sistema al volume iniziale $V_A$. Infine, il gas posto a contatto con la sorgente a temperatura iniziale si riporta alla temperatura $T_2$ tramite una trasformazione isocora irreversibile.

Determinare: a) Il volume in $A$; b) la temperatura $T_2$; c) il lavoro prodotto in un ciclo; d) il rendimento.

(dati del problema $T_1=25{}^{o}C$, $p_A=3.5\cdot 10^{5}Pa$, $p_B=1\cdot 10^{5}Pa$, $V_B=0.02m^3$).

Nota: la irreversibilità della adiabatica è data dal fatto che non tutto il lavoro prodotto è utilizzato, in quanto in parte viene dissipato per  attrito negli ingranaggi esterni al gas. 
Quindi le leggi che governano le adiabatiche dei gas perfetti sono utilizzabili.

10 Cilindro chiuso

Un cilindro chiuso contiene $n$ moli di un gas biatomico a temperatura $T_0$ e pressione $P_0$ . La sezione del cilindro vale $S$ ed inizialmente solo la forza peso del pistone lo tiene in equilibrio (nel contenitore superiore vi è il vuoto), in quanto la molla di costante di richiamo elastico $k$ è a riposo. Il gas viene scaldato ponendolo su una sorgente a temperatura $T_1$ ed il pistone si alza di una quota $h$ e allo stesso tempo la molla si contrae di $h$ raggiungendo una nuova posizione di equilibrio.

Determinare a) la massa $M$ del pistone; b) la pressione $P_1$, il volume $V_1$ e la temperatura $T_1$ finale del gas; c) il calore che il sistema assorbe dalla sorgente.

(Dati del problema $T_0=20{}^{o}C$, $S=0.01m^2$, $P_0=4\cdot 10^{5}Pa$ , $n=0.8moli$, $h=20cm$, $k=5000N/m$ )

Soluzioni

1. Isobara irreversibile

La trasformazione è isobara irreversibile.

Il numero di moli $n$ vale:

$n=\frac{p_0{V}_0}{R{T}_0}=0.066moli$

L'equazione di stato permette di calcolare la temperatura finale $T_1$:

$\frac{p_0{V}_0}{T_0}=\frac{p_{0}2V_0}{T_1}$

$T_1=2T_0=546K$

La variazione di energia interna vale:

$\mathrm{\Delta }U=n{c}_v(T_1-T_0)=375J$

sapendo che:

$c_v=\frac{3}{2}R$

2. Adiabatica gas perfetto

Essendo:

$T_1=273+127=400K$

Dalla relazione:

$T{V}^{\gamma -1}=cost$

segue che essendo $\gamma =1.4$:

$T_f=T_1(0.5{)}^{0.4}=303K$

Quindi l'energia interna è diminuita di:

$DU=\frac{5}{2}R(T_f-T_1)=-2014J$

che è pari (a meno del segno con il lavoro compiuto):

$W=-DU=2014J$

3. Adiabatica con recipiente

Essendo in questo caso, in un intervallo qualsiasi della trasformazione adiabatica reversibile:

$dU=n\frac{3}{2}RdT+\alpha n3RdT$

$pdV=nRT\frac{dV}{V}$

Imponendo la condizione di adiabaticità:

$dU+pdV=0$

$n\frac{3}{2}RdT+\alpha n3RdT+nRT\frac{dV}{V}=0$

separando le variabili:

$\frac{3+6\alpha }{2}\frac{dT}{T}=-\frac{dV}{V}$

Quindi:

$V{T}^{(3+6\alpha )/2}=cost$

$T{V}^{2/(3+6\alpha )}=cost$

Imponendo, come in tutte le adiabatiche che:

$\gamma -1=\frac{2}{3+6\alpha }$

$\gamma =1+\frac{2}{3+6\alpha }$

per $\alpha =0.1$

$\gamma =1.55$

per $\alpha =1$:

$\gamma =1.22$

per $\alpha =10$:

$\gamma =1.03$

4. Ciclo di Stirling

Detti $A$ e $B$ gli estremi della isoterma superiore, e $C$ e $D$ quelli della isoterma inferiore, per le isocore vale:

$V_A=V_D$

$V_B=V_C$

quindi nel caso specifico:

$\frac{V_B}{V_A}=\frac{V_C}{V_D}=2$

Il calore assorbito durante l'isoterma a temperatura più alta vale:

$Q_{AB}=nR{T}_2\ln \frac{V_B}{V_A}=nR{T}_2\ln 2$

Il calore ceduto durante l'isoterma a temperatura più bassa vale:

$Q_{CD}=nR{T}_1\ln \frac{V_D}{V_C}=-nR{T}_1\ln 2$

Il calore scambiato nelle due isocore è sempre eguale e contrario:

$Q_{BC}=-Q_{DA}=n{c}_v(T_1-T_2)$

Quindi il lavoro prodotto è lo stesso nei tre casi:

$W=Q_{AB}+Q_{CD}=nR(T_2-T_1)\ln 2$

a)

Nel primo caso il calore fornito dalla sorgente a temperatura più alta è solo $Q_{AB}$. Vi deve essere un numero infinito di sorgenti tra temperatura $T_1$ e $T_2$ le quali forniscono calore nella isocora in salita ed assorbono la stessa quantità di calore nella isocora in discesa. Quindi:

${\eta }_1=\frac{W}{Q_{AB}}=\frac{nR(T_2-T_1)\ln 2}{nR{T}_2\ln 2}=1-\frac{T_1}{T_2}=0.38$

b)

Nel secondo caso la sorgente a temperatura maggiore deve fornire anche il calore:

$Q_{DA}=n{c}_v(T_2-T_1)$

oltre a $Q_{AB}$ quindi:

${\eta }_2=\frac{W}{Q_{AB}+Q_{DA}}=\frac{(T_2-T_1)\ln 2}{T_2\ln 2+3/2(T_2-T_1)}=0.27$

c)

Nel terzo caso essendovi una sorgente a temperatura intermedia:

$T_3=\frac{T_1+T_2}{2}=405K$

La sorgente a temperatura più alta fornisce una quantità di calore inferiore rispetto al caso b) in quanto deve portare il gas solo da $T_3$ a $T_2$. Quindi il calore fornito vale:

$Q_A=Q_{AB}+n{c}_v(T_3-T_1)$

Il rendimento del ciclo vale:

${\eta }_3=\frac{W}{Q_{AB}+n{c}_v(T_2-T_3)}=\frac{\ln 2(T_2-T_1)}{T_2\ln 2+3/2(T_2-T_3)}=0.3$

5. Ciclo anomalo

a)

Nello stato $C$ essendo $T_C=T_A$, $V_C=2V_A$, dovrà essere $p_C=p_A/2$. Essendo l'elio un gas monoatomico:

$\gamma =1.67$

Nello stato $C$ $p_B=p_A=2p_C$ e quindi:

$p_B{V}_B^{\gamma }=p_C{V}_C^{\gamma }=\frac{p_B}{2}(2V_A{)}^{\gamma }$

$V_B=2V_A(2{)}^{-1/\gamma }=0.0013m^3$

$T_B=2T_A(2{)}^{-1/\gamma }=390K$

b)

Durante la isobara il calore assorbito vale:

$Q_{AB}=n{c}_p(T_B-T_A)=\frac{5}{2}R(T_B-T_A)=1871J$

Durante la adiabatica non viene scambiato calore. Mentre durante la isoterma:

$Q_{CA}=L_{CA}=nR{T}_A\ln \frac{V_A}{V_C}=-1729J$

Quindi il lavoro prodotto per il primo principio della termodinamica vale:

$W_{ciclo}=Q_{AB}+Q_{CA}=142J$

c)

Il rendimento vale:

$\eta =\frac{W_{ciclo}}{Q_{AB}}=0.076$

6. Ciclo irreversibile

a)

Nello stato A la pressione interna al cilindro è pari a:

$P_A=P_{atm}+\frac{Mg}{S}\simeq 1.2\times 10^5\mathrm{P}\mathrm{a}$

e quindi il volume vale:

$V_A=\frac{nR{T}_A}{P_A}\simeq 0.0062{\mathrm{m}}^3$

b)

La trasformazione $A\to B$ è una isocora ($V_B=V_A$, $W=0$) irreversibile nella quale viene raggiunto lo stato B con $T_B$ e pressione

$P_B=\frac{nR{T}_B}{V_A}\simeq 2.02\times 10^5\mathrm{P}\mathrm{a}$

c)

Il calore assorbito dalla sorgente nella trasformazione è pari alla variazione di energia interna del gas:

$Q_{AB}=\mathrm{\Delta }U=n\frac{5}{2}R(T_B-T_A)\simeq 1.26\mathrm{k}\mathrm{J}$

d)

Il pistone si solleva di una altezza:

$h=(V_C-V_B)/S\simeq 2.1m$

Il lavoro compiuto dal sistema contro la pressione esterna $P_A$ è pari a $W_{BC}=P_A(V_C-V_B)=504\mathrm{J}$.

e)

Chiudendo il ciclo con una isobara reversibile $C\to A$ il lavoro assorbito sarebbe eguale a $-W_{BC}$ quindi il rendimento totale del ciclo sarebbe nullo.

7. Trasformazione politropica

a)

Trasformando la temperatura in gradi K:

$T_o=298K$

Essendo la trasformazione politropica (generica reversibile):

$T_o{V}_o^{-3}=T_f(\alpha V_o{)}^{-3}$

$T_f={\alpha }^3{T}_o=818K$

b)

Il lavoro fatto durante la trasformazione vale:

$W=\underset{V_o}{\overset{\alpha V_o}{\int }}pdV=\underset{V_o}{\overset{\alpha V_o}{\int }}\frac{nRT}{V}dV=\frac{nR{T}_o}{V_o^3}\underset{V_o}{\overset{\alpha V_o}{\int }}{V}^{2}dV=\frac{nR{T}_o}{3}({\alpha }^3-1)=1.73kJ$

c)

Essendo:

$c_v=\frac{3}{2}R=12.47J/K$

La variazione di energia interna è:

$\mathrm{\Delta }U=n{c}_v(T_f-T_o)=7.8kJ$

Quindi il calore scambiato dalla trasformazione è:

$Q_a=W+\mathrm{\Delta }U=9.5kJ$

8. Molla e pistone

a)

Sul pistone agiscono la forza dovuta alla pressione del gas e la compressione della molla e le due forze si bilanciano:

$K\mathrm{\Delta }l=P_{o}S$

Detta $P_o$ la pressione iniziale del gas, e $S$ la superficie del cilindro. Valendo l'equazione di stato:

$K\mathrm{\Delta }l=\frac{nR{T}_o}{Sh}S$

$\mathrm{\Delta }l=\frac{nR{T}_o}{Kh}=0.075m$

b)

Nello stato finale il volume del gas diventa:

$V_f=S(h+\mathrm{\Delta }l)$

La condizione di equilibrio diviene:

$p_{f}S=K2\mathrm{\Delta }l=K2\frac{nR{T}_o}{Kh}$

$p_f=\frac{2nR{T}_o}{Sh}$

Quindi:

$T_f=\frac{p_f{V}_f}{nR}=\frac{2nR{T}_{o}S(h+\mathrm{\Delta }l)}{ShnR}=2T_o(1+\mathrm{\Delta }l/h)=824K$

c)

Il lavoro necessario a comprimere la molla vale:

$W=\frac{1}{2}K(2\mathrm{\Delta }l{)}^2-\frac{1}{2}K\mathrm{\Delta }{l}^2=\frac{3}{2}K(\mathrm{\Delta }l{)}^2=420J$

Quindi dal I principio:

$Q_a=\mathrm{\Delta }U+W=n\frac{3}{2}R(T_f-T_o)+W=2390J$

9 Ciclo irreversibile con isocora

a)

Essendo il gas monoatomico:

$\gamma =\frac{5}{3}=1.66$

Essendo la $AB$ trasformazione adiabatica:

$p_A{V}_A^{\gamma }=p_B{V}_B^{\gamma }$

Quindi

$V_A=V_B{\left(\frac{P_B}{P_A}\right)}^{1/\gamma }=0.0094m^3$

b)

Il numero di moli del gas è pari a :

$n=\frac{p_B{V}_B}{R{T}_1}=0.81mol$

Quindi la temperatura in A vale:

$T_2=\frac{p_A{V}_A}{nR}=492K$

Si poteva anche determinare da:

$T_2=T_1(p_B/p_A{)}^{(1-\gamma )/\gamma }=492K$

c)

Il lavoro da compiere durante la isoterma reversibile è pari a

$W_{BC}=nR{T}_1\log V_C/V_B=-1500J$

Mentre il lavoro compiuto durante la adiabatica è pari a:

$W_{AB}=0.9n{c}_v(T_2-T_1)=1760J$

essendo $c_v=3/2R=12.5J/Kmol$. Quindi il lavoro totale vale:

$W=W_{BC}+W_{AB}=260J$

d)

L'unico calore assorbito dalla sorgente a temperatura più alta è quello durante la isocora che vale:

$Q_{CA}=n{c}_v(T_2-T_1)=1952J$

Quindi il rendimento di un ciclo è pari a:

$\eta =\frac{W}{Q_{CA}}=0.13$

10 Cilindro chiuso

a)

La massa del pistone è tale che la sua pressione è pari alla pressione del gas:

$\frac{Mg}{S}=P_0$

quindi:

$M=\frac{P_{0}S}{g}=407kg$

b)

La pressione finale sarà pari a :

$P_1=P_0+\frac{kh}{S}=5\cdot 10^{5}Pa$

Mentre il volume iniziale era:

$V_0=\frac{nR{T}_0}{P_0}=0.0049m^3$

Diviene:

$V_1=V_0+Sh=0.0069m^3$

Quindi la temperatura è:

$T_1=\frac{P_1{V}_1}{nR}=517K$

c)

Detto $c_v=\frac{5}{2}R=20.8J/(molK)$. La variazione di energia interna del gas vale:

$\mathrm{\Delta }U=n{c}_v(T_1-T_0)=3.72kJ$

mentre il lavoro fatto contro la forza peso è:

$L_p=Mgh=800J$

Mentre il lavoro fatto contro la forza elastica vale:

$L_e=\frac{1}{2}k{h}^2=100J$

In totale quindi:

$Q=\mathrm{\Delta }U+L_p+L_e=4.62kJ$