Esercizi di fisica con soluzioni/Statica dei corpi rigidi

Esercizi

1. Scala

Una scala di massa $m$ e lunghezza $l$ è appoggiata ad un estremo ad un muro verticale (liscio) e ad un altro estremo al suolo con coefficiente di attrito ${\mu }_s$. Detto $\theta$ l'angolo che la scala forma con la direzione verticale (si può verificare che la scala da sola è in equilibrio). Un uomo di massa $M$ sale sulla scala, la scala rimane ancora in equilibrio se l'uomo sale fino al gradino più alto?

(dati del problema $m=10kg$, $M=80kg$, ${\mu }_s=0.5$, $\theta =22.5^o$)

2. Asta

Una fune sostiene una trave orizzontale di massa $m/2$, lunga $l=8m$, bloccata ad un estremo da una parete verticale e all'altro è appesa una massa $m=900kg$. La fune è fissata nell'estremo B della trave, quindi non può scorrere, e forma un angolo $\theta =40^o$ con la direzione orizzontale.

Determinare a) la tensione della fune tra il muro e l'asta; b) la componente normale esercitata dalla trave sulla parete; c) il coefficiente minimo di attrito statico tra parete e trave, in maniera che la trave rimanga bloccata alla parete.

3. Mezzo anello

Determinare il centro di massa di un mezzo anello di raggio $R$ e massa $m$ uniforme.

4. Quarto di anello

Determinare il centro di massa di un quarto di anello di raggio $R$ e massa $m$ uniforme.

5. Mezzo disco e mezza sfera

Determinare il centro di massa di un mezzo disco di raggio $R$ e massa $m$ uniforme e di una mezza sfera con le stesse caratteristiche.

6. Quarto di disco

Determinare il centro di massa di un quarto di disco di raggio $R$ e massa $m$ uniforme.

7. Sfera con foro

Determinare il centro di massa di una sfera di raggio $R=70cm$ al cui interno sia stata tolta una sfera di raggio $R/2$ tangente alla sfera maggiore.

8. Disco bloccato

Un disco di massa $m=3kg$ e raggio $R=20cm$ è sottoposto all'azione di una forza $F=20N$ che è applicata ad altezza $R$, poggia su un piano orizzontale scabro ed è trattenuto fermo da un filo disposto come in figura con un angolo $\theta =30^o$ rispetto alla direzione orizzontale.

Determinare a) la tensione del filo; b) il coefficiente di attrito statico minimo che permette l'equilibrio. c) Se la forza viene applicata, più in alto ad altezza $x$, trovare il valore $x$ per cui la forza di attrito è nulla e quindi il piano può essere liscio come si vuole.

9. Manubrio asimmetrico

Una asta rigida di massa trascurabile ha agli estremi due sfere piene di ferro ${\rho }_{Fe}=7.8g/c{m}^3$ di raggio $R_1=2.5cm$ e $R_2=4cm$. Al centro dell'asta un perno (fulcro) nel punto $C$ permette la rotazione del sistema. La distanza tra i centri delle sfere ed il fulcro vale $\ell /2=5cm$. Un filo trattiene la sfera di massa maggiore. Determinare: a) la massa totale del sistema e la posizione del centro di massa rispetto al punto $C$; b) la reazione vincolare del fulcro.

Il filo si spezza e il sistema incomincia a ruotare, determinare c) l'accelerazione angolare del sistema all'istante iniziale del moto; d) la velocità angolare quando l'asta è verticale.

Soluzioni

1. Scala

Detto $A$ il punto di appoggio verticale ed $B$ quello orizzontale; scelto l'asse $x$ come direzione orizzontale e la $y$ come verticale; assunto $B$ come polo. La prima equazione cardinale nella direzione verticale è (detta $N_B$ la reazione vincolare normale al punto B) :

$N_B-mg-Mg=0$

da cui:

$N_B=(m+M)g=882N$

Detta $l_1$ la distanza da $A$ dell'uomo compresa tra $0$ ed $l$, imponendo che il momento delle forze rispetto al polo $B$ sia nullo (detta $N_A$ la reazione vincolare normale al punto A):

$Mg{l}_1\sin \theta +mg\frac{l}{2}\sin \theta -N_{A}l\cos \theta =0$

da cui:

$N_A=\frac{Mg{l}_1\sin \theta +mg\frac{l}{2}\sin \theta }{l\cos \theta }=\tan \theta g(M\frac{l_1}{l}+\frac{m}{2})$

Che è massima quando:

$l_1=l$

cioè per:

$N_A=\tan \theta g(M+\frac{m}{2})=345N$

Per avere equilibrio occorre che anche, ( detta $f_{aB}$ la forza di attrito statico tra il punto nel punto B):

$N_A+f_{aB}=0$

quindi

$f_{aB}=-345$

La condizione di equilibrio è verificata infatti:

$|f_{aB}|\le |{\mu }_s{N}_B|=440N$

2. Asta

a)

Imponendo che sia nullo il momento totale delle forze, rispetto all'estremo sulla parete:

$mgl+\frac{m}{2}g\frac{l}{2}-Tl\sin \theta =0$

segue che:

$T=\frac{mg}{\sin \theta }(1+\frac{1}{4})=17\cdot 10^{3}N$

b)

La componente normale della reazione vincolare della parete alla compressione vale:

$N=T\cos \theta =13\cdot 10^{3}N$

c)

Le forze verticali agenti sulla trave ad esclusione della reazione vincolare sono:

$F_y=-mg-\frac{mg}{2}+T\sin \theta =-\frac{mg}{4}=-2.2\cdot 10^{3}N$

Quindi, dovendo essere:

${\mu }_{s}N+F_y=0$

Il minore coefficiente di attrito statico che garantisce il blocco della trave vale:

${\mu }_s=-\frac{F_y}{N}=0.17$

3. Mezzo anello

Scegliamo l'origine e gli assi come in figura.

La densità lineare di massa vale:

$\lambda =\frac{m}{\pi R}$

Mentre l'elemento di lunghezza infinitesima, assunto come variabile l'angolo $\theta$, è:

$dl=Rd\theta$

Quindi:

$dm=\lambda dl=\frac{m}{\pi R}Rd\theta =\frac{m}{\pi }d\theta$

Tale generico elemento di trova nel punto di coordinate:

$(x^{\prime },y^{\prime })=(R\sin \theta ,R\cos \theta )$

Quindi:

$x_{CM}=\frac{\underset{-\pi /2}{\overset{+\pi /2}{\int }}{x}^{\prime }dm}{m}=\frac{\underset{-\pi /2}{\overset{+\pi /2}{\int }}R\sin \theta \frac{m}{\pi }d\theta }{m}=\frac{R}{\pi }{[-\cos \theta ]}_{-\pi /2}^{+\pi /2}=0$

come era ovvio per ragioni di simmetria. Mentre:

$y_{CM}=\frac{\underset{-\pi /2}{\overset{+\pi /2}{\int }}{y}^{\prime }dm}{m}=\frac{\underset{-\pi /2}{\overset{+\pi /2}{\int }}R\cos \theta \frac{m}{\pi }d\theta }{m}=\frac{R}{\pi }{[\sin \theta ]}_{-\pi /2}^{+\pi /2}=\frac{2R}{\pi }$

4. Quarto di anello

Scegliamo l'origine e gli assi come in figura.

La densità lineare di massa vale:

$\lambda =\frac{2m}{\pi R}$

Mentre l'elemento di lunghezza infinitesima, assunto come variabile l'angolo $\theta$, è:

$dl=Rd\theta$

Quindi:

$dm=\lambda dl=\frac{2m}{\pi R}Rd\theta =\frac{2m}{\pi }d\theta$

Tale generico elemento di trova nel punto di coordinate:

$(x^{\prime },y^{\prime })=(R\sin \theta ,R\cos \theta )$

Quindi:

$x_{CM}=\frac{\underset{0}{\overset{\pi /2}{\int }}{x}^{\prime }dm}{m}=\frac{\underset{0}{\overset{\pi /2}{\int }}R\sin \theta \frac{2m}{\pi }d\theta }{m}=\frac{2R}{\pi }{[-\cos \theta ]}_0^{\pi /2}=\frac{2R}{\pi }$

Che coincide numericamente come si poteva aspettare per ragioni di simmetria con il valore dell'altro asse:

$y_{CM}=\frac{\underset{0}{\overset{\pi /2}{\int }}{y}^{\prime }dm}{m}=\frac{\underset{0}{\overset{\pi /2}{\int }}R\cos \theta \frac{2m}{\pi }d\theta }{m}=\frac{2R}{\pi }{[\sin \theta ]}_0^{\pi /2}=\frac{2R}{\pi }$

5. Mezzo disco e mezza sfera

a) Mezzo disco

Scegliamo l'origine e gli assi come in figura.

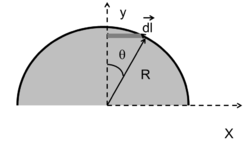
La densità superficiale di massa vale:

$\sigma =\frac{2m}{\pi R^2}$

L'elemento di superficie infinitesimo è alto (larghezza della striscia più scura in figura):

$dh=Rd\theta \sin \theta$

ed ha una lunghezza:

$l=R\sin \theta$

L'elemento di superficie infinitesimo dS (striscia più scura in figura) è un rettangolo di superficie:

$dS=ldh=R^2{\sin }^2\theta d\theta$

Quindi:

$dm=\sigma dS=\frac{2m}{\pi R^2}{R}^2{\sin }^2\theta d\theta =\frac{2m}{\pi }{\sin }^2\theta d\theta$

Quindi il generico elemento di superficie si trova ad una quota:

$h=R\cos \theta$

Quindi la posizione del centro di massa sull'asse delle y (la coordinata x per simmetria è nulla) vale:

$y_{CM}=\frac{\underset{-\pi /2}{\overset{\pi /2}{\int }}hdm}{m}=\frac{\underset{-\pi /2}{\overset{+\pi /2}{\int }}R\cos \theta \frac{2m}{\pi }{\sin }^2\theta d\theta }{m}=\frac{2R}{\pi }\underset{-\pi /2}{\overset{\pi /2}{\int }}{\sin }^2\theta (d\sin \theta )=\frac{2R}{\pi }{\left[\frac{{\sin }^3\theta }{3}\right]}_{-\pi /2}^{+\pi /2}=\frac{4R}{3\pi }$

b) Semisfera

La densità (volumetrica) di massa vale:

$\rho =\frac{3m}{2\pi R^3}$

L'elemento di lunghezza infinitesima, è alto (larghezza del striscia più scura in figura):

$dh=Rd\theta \sin \theta$

L'elemento di volume infinitesimo dV (striscia più scura in figura) è un disco di altezza dh e raggio

$r=R\sin \theta$

Quindi:

$dV=\pi R^3{\sin }^3\theta d\theta$

Quindi:

$dm=\rho dV=\frac{3m}{2\pi R^3}\pi R^3{\sin }^3\theta d\theta =\frac{3m}{2}{\sin }^3\theta d\theta$

Quindi il generico elemento di volume si trova ad una quota:

$h=R\cos \theta$

La coordinata y del centro di massa (la x e la z sono nulle per ragioni di simmetria) vale:

$y_{CM}=\frac{\underset{0}{\overset{\pi /2}{\int }}hdm}{m}=\frac{\underset{0}{\overset{\pi /2}{\int }}R\cos \theta \frac{3m}{2}{\sin }^3\theta d\theta }{m}=\frac{3}{2}R\underset{0}{\overset{\pi /2}{\int }}{\sin }^3\theta (d\sin \theta )=\frac{3}{2}R{\left[\frac{{\sin }^4\theta }{4}\right]}_0^{\pi /2}=\frac{3}{8}R$

6. Quarto di disco

a) Mezzo disco

Scegliamo l'origine e gli assi come in figura.

La densità superficiale di massa vale:

$\sigma =\frac{4m}{\pi R^2}$

L'elemento di lunghezza infinitesima è alto (larghezza della striscia più scura in figura):

$dh=Rd\theta \sin \theta$

L'elemento di superficie infinitesimo dS (striscia più scura in figura) è un rettangolo di altezza dh e di lunghezza

$l=R\sin \theta$

Quindi:

$dS=R^2{\sin }^2\theta d\theta$

Quindi:

$dm=\sigma dS=\frac{2m}{\pi R^2}{R}^2\sin \theta d\theta =\frac{2m}{\pi }\sin \theta d\theta$

Quindi il generico elemento di superficie si trova ad una quota:

$h=R\cos \theta$

Quindi la posizione del centro di massa sull'asse delle y vale:

$y_{CM}=\frac{\underset{0}{\overset{\pi /2}{\int }}hdm}{m}=\frac{\underset{0}{\overset{\pi /2}{\int }}R\cos \theta \frac{4m}{\pi }{\sin }^2\theta d\theta }{m}=\frac{2R}{\pi }\underset{0}{\overset{\pi /2}{\int }}{\sin }^2\theta (d\sin \theta )=\frac{4R}{\pi }{\left[\frac{{\sin }^3\theta }{3}\right]}_0^{\pi /2}=\frac{4R}{3\pi }$

Costruendo un rettangolo verticale invece che orizzontale e ripetendo lo stesso ragionamento si ha che anche:

$x_{CM}=\frac{4R}{3\pi }$

7. Sfera con foro

Detto $\rho$ la densità, il problema diventa equivalente ad una sfera uniforme di raggio $R$ e densità $\rho$ ed una sfera di raggio $R/2$ posta nel punto $R/2$ ma con densità $-\rho$. Quindi la posizione del $CM$ sull'asse congiungente i due centri vale:

$r_{CM}=\frac{-\rho \frac{4}{3}\pi (R/2{)}^3\frac{R}{2}}{\frac{4}{3}\rho \pi [R^3-(R/2{)}^3]}=-\frac{1}{14}R=-3.5cm$

8. Disco bloccato

Sul disco agiscono quattro forze la forza peso, la tensione del filo, la reazione vincolare e la forza esterna.

a)

Scomponiamo la reazione vincolare in una componente normale al piano $R_n$ ed una orizzontale $f$. La condizione di equilibrio per le forze, sull'asse orizzontale:

$F+T\cos \theta +f=0$

Per quanto riguarda i momenti rispetto al baricentro (positivo antiorario):

$TR\sin \theta -fR=0$

Eliminando $f$:

$T=-\frac{F}{\cos \theta +\sin \theta }=-14.6N$

b)

$f=T\sin \theta =-7.3N$

per quanto riguarda la reazione vincolare normale:

$R_n=-mg-T\sin \theta =37N$

Imponendo che:

$|f|\le {\mu }_s{R}_n$

${\mu }_s\ge 0.2$

c)

Se la forza è applicata in $x$ la risultante delle forze orizzontali ha la stessa espressione anche se la tensione è diversa:

$F+T_x\cos \theta +f_x=0$

Il pedice $T_x$ è il modulo della tensione ed $f_x$ è la forza di attrito statico se $F$ è applicato nel punto ad altezza $x$. Per quanto riguarda i momenti rispetto al baricentro invece:

$T_{x}R\sin \theta -F(x-R)-f_{x}R=0$

Eliminando $T_x$:

$f_x=\frac{F(x-R-R\tan \theta )}{R(1+tan\theta )}$

Che è nulla per

$x-R-R\tan \theta =0$

$x=0.315m=31.5cm$

9. Manubrio asimmetrico

a)

La massa della sfera più piccola è:

$M_1=\frac{4}{3}\pi R_1^3{\rho }_{Fe}=0.51kg$

mentre di quella maggiore:

$M_2=\frac{4}{3}\pi R_2^3{\rho }_{Fe}=2.1kg$

Quindi:

$M=M_1+M_2=2.6kg$

Il centro di massa del sistema è a destra del fulcro a distanza:

$x_{CM}=\frac{-M_1\ell /2+M_2\ell /2}{M}=0.03m$

b)

Per avere equilibrio il momento delle forze rispetto a $C$ deve essere nullo quindi, detta $T_2$ la tensione del filo, deve essere:

$T_2\frac{\ell }{2}=Mg{x}_{CM}$

quindi:

$T_2=\frac{Mg{x}_{CM}2}{\ell }=15.5N$

Chiamiamo $T_1$ la reazione vincolare del perno (diretta seconda la verticale). Dovendo essere la risultante delle forze nulle:

$Mg=T_1+T_2$

$T_1=Mg-T_2=10N$

c)

Il momento di inerzia della sfera di sinistra rispetto al fulcro vale:

$I_1=\frac{2}{5}{M}_1{R}_1^2+M_1\frac{{\ell }^2}{4}=0.0014kg{m}^2$

Il momento di inerzia della sfera di destra rispetto al fulcro vale:

$I_2=\frac{2}{5}{M}_2{R}_2^2+M_2\frac{{\ell }^2}{4}=0.0066kg{m}^2$

Quindi il momento di inerzia totale vale:

$I=I_1+I_2=0.008kg{m}^2$

Quando si spezza il filo dalla seconda equazione cardinale:

$I\alpha =Mg{x}_{CM}$

$\alpha =\frac{Mg{x}_{CM}}{I}=97rad/s^2$

d)

Nel punto più basso l'energia potenziale del sistema è diventata cinetica:

$\frac{1}{2}I{\omega }^2=Mg{x}_{CM}$

$\omega =\sqrt{\frac{2Mg{x}_{CM}}{I}}=13.9rad/s$