Fisica classica/Leggi di Laplace

Template:Capitolo Template:Fisica classica

La seconda legge di Laplace

Un filo percorso da una corrente I in un campo magnetico entrante nel piano del foglio

Una osservazione sperimentale dovuta a Gian Domenico Romagnosi, permette di collegare il campo di induzione magnetica alla corrente elettrica.

Consideriamo un campo di induzione magnetica entrante nel foglio (per convenzione le croci indicano tale fatto: richiamano infatti la coda di una freccia)

Consideriamo un filo percorso da una corrente $I$ lungo $\vec{d l}$ come in figura: se la direzione del filo è ortogonale alla direzione del campo magnetico sperimentalmente si trova che la forza che agisce su di esso sarà mutuamente perpendicolare sia alla direzione del campo magnetico che alla direzione del filo e proporzionale all'intensità della corrente ed alla lunghezza del filo.

In figura è mostrato un generatore di f.e.m. che fa scorrere la corrente nel circuito indicato. Nel piano normale al filo vi è un campo magnetico di intensità $| B |$ (entrante nel foglio, per questo indicato con le x). Una parte del circuito di lunghezza $d l$ è mobile e trattenuto da delle molle: si misura una forza nella direzione indicata.

Si può quindi definire il campo di induzione magnetica, a partire da tale forza $\vec{F}$ misurabile, come:

| B | = \frac{| F |}{I | d l |}

quindi nel sistema MKSA il campo di induzione magnetica si misura in Tesla definito come:

[B] = \frac{[N]}{[A] [m]} = [T]

Se il filo è parallelo alle linee del campo su di esso in generale non agisce nessuna forza. L'espressione matematica della forza di un campo magnetico su un filo percorso da corrente viene detta seconda legge di Laplace:

\vec{d F} = I \vec{d l} \times \vec{B}

La così detta regola della mano destra può essere di aiuto nel calcolo della direzione della forza agente. Infatti, se la direzione della corrente è quella dell'indice della mano destra e quella del campo magnetico è il medio, la direzione della forza è data dalla direzione del pollice.

Il campo magnetico terrestre può dare un'idea dell'intensità tipiche: alla nostra latitudine ( $4 2^{o}$ ) vale circa $6 \times 1 0^{- 5} T$ . Il campo magnetico prodotto da un magnete permanente tradizionale difficilmente supera il valore di $1 T$ . Campi magnetici più intensi si raggiungono mediante magneti superconduttori, ma difficilmente in condizioni statiche si riescono ad avere intensità maggiori di $25 T$ . Esistono delle stelle di neutroni dette magnetar con campi magnetici particolarmente intensi superiori a Template:M.

Il motore lineare

L'applicazione più semplice della II seconda equazione di Laplace è il motore lineare. Cioè due rotaie percorse da una corrente $I$ come in figura, in cui il vagone conduttore chiude la corrente circolante. Un campo magnetico uniforme viene applicato nella direzione normale al piano delle rotaie. Sul vagone agisce una forza di trascinamento proporzionale all'intensità del campo, alla corrente ed alla distanza tra le rotaie.

Questa tecnica è impiegata in sistemi di trasporto a levitazione magnetica, come i treni maglev installati a Shanghai (il primo nato), a Vancouver e Toronto in Canada, all'aeroporto JFK di New York e a Kuala Lampur in Malesia. Il sistema è usato anche in alcune montagne russe ed è stato proposto in esecuzione verticale come ascensore per i pozzi delle miniere.

I motori elettrici in generale, che funzionano sull'estensione a geometrie più complesse dei principi di funzionamento del motore lineare, sono basati sulla conversione della energia prodotta dai generatori di f.e.m. in energia meccanica: si noti che il campo magnetico non compie lavoro, ma è solo il generatore di f.e.m. a farlo.

Forza di Lorentz

L'espressione della seconda legge di Laplace ci permette di trovare la forza agente su una singola carica in moto.

Dal modello microscopico sappiamo che il prodotto di una corrente elettrica per il tratto di filo elementare $\vec{d l}$ in cui scorre, può essere scritta come:

I \vec{d l} = \vec{J} \cdot \vec{S} \vec{d l} = n q \vec{v} | S | | d l | = Δ N q \vec{v}

dove $\vec{J}$ è la densità di corrente, $\vec{S}$ è un vettore normale alla sezione del filo di modulo pari alla sezione stessa, $n$ è il numero dei portatori di carica per unità di volume, $\vec{v}$ la loro velocità, $q$ la loro carica ed infine $Δ N = n S d l$ il loro numero nel volume $S d l$ .

Sostituendo questa equazione nella seconda legge di Laplace, troviamo che la forza che agisce su una singola carica $q$ che si muova con velocità $\vec{v}$ in un campo di induzione magnetica $\vec{B}$ sia:

\vec{F} = q \vec{v} \times \vec{B}

In generale se quindi la particella carica si muove in un campo elettrico $\vec{E}$ e magnetico $\vec{B}$ l'espressione generale della forza, detta di Lorentz, che agisce su di essa, vale:

\vec{F} = q (\vec{E} + \vec{v} \times \vec{B})

Moto di cariche in campi magnetici

Moto di una carica in un campo magnetico

Supponiamo di avere una regione di spazio, dove $\vec{B}$ è costante. In essa si trova una particella di massa $m$ , carica $q$ (positiva) e con velocità $v$ normale alla direzione di $\vec{B}$ (entrante nel piano della figura). A causa della forza di Lorentz agirà su di essa una forza normale alla traiettoria (che non compie lavoro in quanto centripeta). In condizioni di equilibrio dinamico, essendo l'accelerazione centripeta costante il moto nel piano normale al campo sarà un moto circolare uniforme con raggio di curvatura $R$ facilmente ricavabile dalla relazione:

q v B = \frac{m v^{2}}{R}

da cui:

R = \frac{m v}{q B}

la velocità angolare è quindi pari a:

ω = \frac{v}{R} = \frac{q B}{m}

Al cambiare di segno della carica il raggio di curvatura cambia di segno e il moto, se era anti orario, diventa orario. Anche al cambiare del segno di $\vec{B}$ il verso del moto si inverte.

La velocità angolare del moto non dipende dalla velocità della particella e la frequenza associata prende il nome di frequenza di ciclotrone. Gran parte delle conoscenze sulle particelle elementari dipende dallo studio del loro moto in presenza di campi elettrici e magnetici.

I raggi cosmici non raggiungono alle nostre latitudini la superficie della terra grazie all'esistenza del campo magnetico terrestre che ne incurva la traiettoria. Nei televisori a tubi catodici, oramai superati tecnologicamente, la deflessione del fascio di elettroni che produce la scansione dell'immagine secondo righe e colonne viene fatta utilizzando dei campi magnetici perpendicolari alla traiettoria iniziale degli elettroni.

Se la velocità iniziale della particella ha una componente nella direzione di $\vec{B}$ solo sulla componente di $\vec{v}$ perpendicolare a $\vec{B}$ agisce la forza di Lorentz, l'altra componente è non modificata, per cui il moto all'equilibrio diventa un moto elicoidale con asse la direzione di $\vec{B}$ . La forza di Lorentz può essere nulla se:

\vec{E} + \vec{v} \times \vec{B} = 0

Cioè se $\vec{E}$ è normale alla direzione di $\vec{v}$ e di $\vec{B}$ e inoltre in modulo:

v = \frac{| E |}{| B |}

Basato su questo principio si riescono a selezionare con estrema precisione ioni di massa qualsiasi in funzione della loro velocità. Infatti solo gli ioni che viaggiano su una traiettoria rettilinea riescono ad attraversare delle strette fenditure allineate.

L'esempio di un elettrone in moto dentro un campo magnetico chiarisce meglio quanto detto.

Azione del campo magnetico su circuiti percorsi da corrente

Schema di una spira rettangolare libera di ruotare all'interno di un campo magnetico uniforme

I motori elettrici in corrente continua utilizzano in pratica quanto viene descritto nel seguito.

Consideriamo il caso particolare, mostrato in figura, di una spira rettangolare di lato $L_{x}$ ed $L_{y}$ (non indicato nella figura per evitare confusione), percorsa da corrente $I$ (circolante in senso antiorario) e con i lati paralleli agli assi $x$ ed $y$ . Immaginiamo che sia presente un campo magnetico $\vec{B}$ diretto secondo l'asse $x$ . Assumiamo la spira rigida e libera di ruotare intorno all'asse $y$ della figura. Concentriamo la nostra attenzione sulla interazione tra spira e campo.

Sui due lati della spira di lunghezza $L_{x}$ non agisce nessuna forza essendo paralleli al campo magnetico. Viceversa sugli altri due lati agiscono due forze eguali e contrarie dirette lungo l'asse $z$ sul lato in alto:

F_{z} = I B L_{y}

sul lato opposto agisce una forza pari a:

F_{z} = - I B L_{y}

Quindi, la risultante è nulla, ma sul centro del sistema rigido agisce una coppia di momento:

M_{y} = I B L_{y} \frac{L_{x}}{2} + I B L_{y} \frac{L_{x}}{2} = I L_{x} L_{y} B

Tale momento fa ruotare il sistema intorno all'asse $y$ . Se la spira aveva una orientazione diversa dobbiamo considerare l'angolo $θ$ che la normale al piano della spira forma con la direzione del campo magnetico. L'espressione del momento della forza diviene (il braccio diminuisce via via che la spira ruota e l'asse della spira si allinea con il campo magnetico):

| M | = I | B | L_{x} L_{y} \sin θ

Notiamo come sui lati diretti in direzione perpendicolare alla direzione dell'asse di rotazione, la forza che agisce è nulla solo quando tali assi sono paralleli al campo. La forza risultante che si ha su detti lati è nella direzione del piano della spira: se la spira è rigida non hanno alcun effetto sulla dinamica. Se si definisce momento di dipolo di una spira percorsa dalla corrente $I$ il vettore:

\vec{m} = I L_{x} L_{y} \vec{n} = I S \vec{n}

Dove $S$ è la superficie della spira ed $\vec{n}$ è la normale ad essa. La regola della mano destra ci può aiutare nel definire la direzione del dipolo magnetico. Se infatti la corrente elettrica si avvolge come fanno le dita della mano destra, la direzione di $\vec{m}$ è quella del pollice della mano stessa. Ovviamente se il verso è opposto opposta sarà la direzione del dipolo magnetico.

Le dimensioni del momento di dipolo magnetico sono quindi quelle di:

[c o r r e n t e] [s u p e r f i c i e]

quindi nel sistema SI:

[A] \cdot [m]^{2}

La coppia di forze che agisce su una spira rettangolare è quindi esprimibile come, il prodotto vettoriale di $\vec{m}$ con il vettore induzione magnetica $\vec{B}$ :

\vec{M} = \vec{m} \times \vec{B}

L'effetto di un campo magnetico su un dipolo magnetico permanente è analogo a quello provocato su una spira percorsa da corrente. Tale equivalenza di comportamento risulta valida anche per i campi magnetici generati dai dipoli magnetici, cosa che vedremo nel seguito: tale equivalenza prende nome di teorema di equivalenza di Ampère.

Una spira di momento di dipolo magnetico $\vec{m}$ , immersa in un campo magnetico uniforme $\vec{B}$ è quindi soggetta ad una coppia di forze di momento $\vec{M} = \vec{m} \times \vec{B}$ .

Motore in corrente continua

L'applicazione più importante di tale proprietà è il motore in corrente continua, che permette di trasformare l'energia elettrica in energia meccanica.

La corrente elettrica passa in un avvolgimento di spire che si trova nel rotore. Si definisce rotore l'insieme delle parti rotanti, libere di ruotare attorno ad un asse comune, il rotore comprende una bobina di fili conduttori detta comunemente avvolgimento. Una corrente elettrica continua alimenta l'avvolgimento. Il rotore è immerso in un campo magnetico creato dallo statore: l'insieme delle parti fisse. Lo statore contiene le espansioni polari o di un magnete permanente con due o più poli o una elettromagnete.

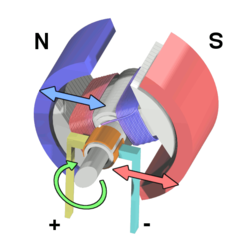
Se il momento magnetico dell'avvolgimento del rotore non è diretto inizialmente nella direzione del campo magnetico dello statore, su di esso agirà una coppia di forze tale da farlo ruotare nel verso che corrisponde all'allineamento del momento magnetico dell'avvolgimento con il campo magnetico dello statore. Grazie alle spazzole o una commutazione elettronica ad ogni mezzo giro il verso della corrente circolante nell'avvolgimento cambia di verso, e quindi si ha continuità nella rotazione. In un motore a spazzole, il contatto meccanico delle spazzole con il collettore rotante sull'asse del rotore chiude il circuito elettrico tra l'alimentazione e gli avvolgimenti sul rotore invertendo periodicamente il verso di circolazione della corrente nelle spire e realizzando così l'inversione delle forze elettrodinamiche che agiscono sulle spire degli avvolgimenti rotorici. Nei motori senza spazzole la commutazione della corrente circolante negli avvolgimenti dello statore, e quindi la variazione dell'orientamento del campo magnetico da essi generato, avviene elettronicamente.

La coppia agente sul rotore dipende dalla sua posizione angolare, il momento di inerzia del rotore media in qualche maniera il momento motore variabile. Un motore in corrente continua non può iniziare a ruotare se l'avvolgimento del rotore si trova in una posizione angolare non opportuna (punto morto). Ma vi sono accorgimenti tecnici per ovviare a tale inconveniente. Il prodotto della tensione di alimentazione per la corrente che circola rappresenta la potenza assorbita per effetto Joule, ma in parte l'energia elettrica viene dissipata in calore e in parte è trasformata in energia meccanica. Un motore elettrico in corrente continua fa muovere l'albero motore di moto rotatorio.

Effetto Hall

Sperimentalmente si ha che in una lastra di metallo o meglio di un semiconduttore immersa in un campo magnetico, se viene percorsa da una corrente nella direzione perpendicolare al campo magnetico, sulla faccia perpendicolare alla direzione sia della corrente che del campo magnetico si sviluppa una differenza di potenziale. La forza di Lorentz spiega in maniera semplice tale effetto.

Per semplicità consideriamo una caso di facile studio, una lastrina di metallo o semiconduttore di spessore $h$ , larghezza $w$ e lunghezza $l$ (la lunghezza non è mostrata nella figura a fianco) attraversata nella direzione $x$ da una corrente elettrica (caratterizzata per quanto abbiamo visto in elettrodinamica da una velocità di drift ${\vec{v}}_{d}$ ). Se nella direzione dello spessore della lastra applichiamo un campo magnetico, questo tende a deviare la traiettoria degli elettroni aumentando la loro densità nella direzione della lastrina non visibile in figura. Tale processo di accumulo di cariche genera nella direzione $y$ un campo elettrico che si oppone alla forza di Lorentz; si raggiunge la condizione di equilibrio dinamico quando:

E_{y} - v_{d} B_{z} = 0

Il segno $-$ in ${\vec{v}}_{d}$ tiene conto del fatto che gli elettroni essendo di carica negativa hanno una velocità di drift opposta alla direzione della corrente elettrica. Sostituendo l'espressione della densità di corrente:

E_{y} = \frac{J_{x} B_{z}}{n e}

Tale campo elettrico è costante nella direzione $y$ e quindi integrandolo si ha che tra la faccia posteriore e anteriore della lastra si sviluppa una d.d.p. pari a:

V_{y} = - \frac{J_{x} B_{z} w}{n e}

Ma la densità di corrente è pari a: $J_{x} = I / (w h)$ . Quindi:

V_{y} = - \frac{I B_{z}}{h n e}

Dalla conoscenza del campo magnetico, dalla misura della differenza di potenziale e dalla corrente che scorre all'interno della piastrina è possibile misurare la quantità microscopica $1 / (n e)$ . Tale quantità viene chiamata costante di Hall $R_{H}$ ed in algebricamente è pari a:

R_{H} = \frac{V_{y} h}{I B_{z}} = - \frac{1}{n e}

La costante di Hall dipende dal segno dei portatori di carica e nel caso dei semiconduttori l'effetto Hall, a causa del numero ridotto di portatori di carica, è particolarmente vistoso: cioè con correnti relativamente piccole e in presenza di campi magnetici abbastanza deboli le differenze di potenziale che si sviluppano possono essere facilmente misurate. Al contrario nei metalli l'effetto è poco visibile, anche se storicamente a metà dell'800 è stato trovato in lastre sottilissime di oro. L'effetto Hall oltre ad essere una misura di routine per determinare il drogaggio dei semiconduttori, viene usato per fabbricare semplici ed economici magnetometri che prendono il nome di sonde di Hall.

La prima legge di Laplace

J. B. Biot e F. Savart trovarono sperimentalmente che un filo rettilineo percorso da corrente $i$ genera nello spazio circostante un campo magnetico. Le linee del campo sono delle circonferenze concentriche al filo e la loro intensità diminuisce linearmente con la distanza $r$ dal filo. A partire da questa osservazione sperimentale si ha una legge di valore più generale che lega la corrente $i$ che scorre in un tratto infinitesimo $\vec{d s}$ di circuito elettrico al campo di induzione magnetica $\vec{d B}$ in un punto a distanza $\vec{r}$ dal filo:

\vec{d B} = \frac{μ_{\circ} i}{4 π} \frac{\vec{d s} \times \vec{r}}{r^{3}} = \frac{μ_{\circ} i}{4 π} \frac{\vec{d s} \times {\hat{u}}_{r}}{r^{2}}

Tale legge prende il nome di I legge di Laplace, chiamata anche legge di Biot-Savart, ed evidenzia come il campo di induzione magnetica varii con il quadrato dell'inverso della distanza, come la legge di Coulomb, ma con un carattere vettoriale molto differente. Infatti le componenti del campo di induzione magnetica sono nulle nella direzione radiale. Le linee del campo sono delle circonferenze concentriche alla direzione del filo.

La quantità $μ_{\circ}$ è chiamata permeabilità magnetica del vuoto le sue dimensioni sono:

\frac{[B] [L u n g h e z z a]}{[C o r r e n t e]}

nel sistema SI $μ_{\circ}$ vale:

μ_{\circ} = 4 π \cdot 1 0^{- 7} \frac{T \cdot m}{A}

Ma si ha anche:

c = \frac{1}{\sqrt{ϵ_{o} μ_{\circ}}}

dove $c$ è la velocità della luce nel vuoto. Siccome nel Sistema Internazionale la velocità della luce è una grandezza definita a priori in maniera esatta ( $c = 299792458 m s^{- 1}$ ), possiamo anche esprimere la permeabilità magnetica nel vuoto come:

μ_{\circ} = \frac{1}{ϵ_{o} c^{2}} T \cdot m / A

Il legame tra $c$ e $ϵ_{o}$ , $μ_{\circ}$ non è casuale, ma implica il forte legame tra elettromagnetismo e teoria della relatività ristretta come appare più palese nell'ultima parte di questo capitolo.

Campo di induzione magnetica di un circuito elettrico

Il campo di induzione magnetica prodotta da un circuito filiforme $L$ , tale cioè che la densità di corrente si possa considerare costante sulla sua sezione, può essere ottenuto integrando la I formula di Laplace lungo $L$ . Infatti se definiamo $I$ la corrente che circola nel circuito segue che:

\vec{B} = \frac{μ_{\circ}}{4 π} I \oint_{L} \frac{\vec{d s} \times \vec{r}}{r^{3}}

Tale espressione è una generalizzazione della I legge di Laplace e prende il nome di equazione di Biot-Savart (dal punto di vista storico è stata derivata per prima).

Campo di induzione magnetica di un filo rettilineo

Un'applicazione classica della legge di Biot-Savart è il calcolo del campo prodotto da un filo rettilineo. Sia dato un filo rettilineo, come in figura, nel quale scorra una corrente $I$ . Si voglia calcolare l'induzione magnetica in un qualsiasi punto $P$ dello spazio a distanza $R$ dal filo.

Scegliamo come asse $z$ (con versore $\vec{k}$ ) il filo stesso e come origine l'intersezione del filo con la normale passante per $P$ . Se come asse $x$ scegliamo la normale al filo passante per il punto $P$ avremo che:

\vec{r} = (R, 0, z) \vec{d s} = (0, 0, d z) \vec{d s} \times \vec{r} = R d z \vec{j}

Il campo di induzione magnetica prodotto sarà quindi, applicando la equazione di Biot-Savart:

\vec{B} = \frac{μ_{\circ}}{4 π} I \oint_{L} \frac{\vec{d s} \times \vec{r}}{r^{3}} = \frac{μ_{\circ}}{4 π} I \int_{- \infty}^{\infty} \frac{R d z \vec{j}}{{(R^{2} + z^{2})}^{3 / 2}}

Sostituendo la espressione analitica dell'integrale precedente:

\vec{B} = \frac{μ_{\circ} I \vec{j}}{4 π R} {[\frac{z}{\sqrt{R^{2} + z^{2}}}]}_{- \infty}^{\infty} = \frac{μ_{\circ} I}{2 π R} \vec{j} = \frac{μ_{\circ} I}{2 π R} \vec{k} \times \vec{i}

Quindi il campo di induzione magnetica prodotto da un filo molto lungo e rettilineo genera un campo magnetico diretto secondo circonferenze concentriche al filo. Tale campo diminuisce linearmente con la distanza dal filo stesso. La regola della mano destra, anche in questo caso, può essere di aiuto; infatti se la corrente è indicata dal pollice della mano destra le linee del campo sono rappresentate dalle altre dita della stessa mano. In genere per un qualsiasi circuito filiforme, per punti estremamente vicini al filo, il campo di induzione magnetica è approssimabile con quello di un filo infinitamente lungo. In realtà vi è da aggiungere che sperimentalmente Biot e Savart trovarono che il campo magnetico di un filo rettilineo è l'espressione qui data e in seguito fu derivata la prima equazione di Laplace.

Campo sull'asse di una spira circolare

Una spira circolare percorsa da corrente, l'elemento di filo è stato definito come dl

Consideriamo una spira di raggio $R$ con asse $z$ coincidente con l'asse della spira e con origine nel centro della spira stessa. L'elemento $d \vec{l}$ genera un campo:

d \vec{B} = \frac{μ_{\circ}}{4 π} I \frac{\vec{d l} \times \vec{r}}{r^{3}}

Infatti $d \vec{l}$ è sempre ortogonale a $\vec{r}$ ; ma, sull'asse di simmetria, per ogni elemento $d \vec{l}$ ne esiste uno diametralmente opposto che dà un contributo a $d \vec{B}$ eguale in modulo al precedente, ma con componente ortogonale a $z$ opposta.

Pertanto il campo $\vec{B}$ risultante sarà diretto secondo l'asse delle $z$ ed il suo valore sarà pari alla somma delle componenti $d B_{z}$ . Essendo:

d B_{z} = | d \vec{B} | \sin α = | d B | \frac{R}{r}

Quindi, in totale:

B_{z} = \oint d B_{z} = \oint \frac{μ_{\circ}}{4 π} I \frac{| d l |}{r^{2}} \frac{R}{r} = \frac{μ_{\circ}}{4 π} I \frac{R}{r^{3}} 2 π R

Considerando un punto sull'asse, a distanza $z$ dall'origine, si ottiene:

r^{2} = R^{2} + z^{2}

B_{z} = \frac{μ_{\circ}}{2 π (R^{2} + z^{2})^{3 / 2}} π I R^{2}

Che con la definizione data di $\vec{m} = I π R^{2} \hat{n}$ si può anche scrivere:

\vec{B} = \frac{μ_{\circ} \vec{m}}{2 π (R^{2} + z^{2})^{3 / 2}}

L'espressione a grande distanza è formalmente eguale a quella di un dipolo elettrico. Si può dimostrare con un conto numerico che in generale, un spira percorsa da corrente o un dipolo magnetico con momento magnetico $\vec{m}$ , a distanza grande rispetto alle dimensioni fisiche dell'oggetto generano un campo di induzione magnetica pari a:

\vec{B} = \frac{μ_{\circ}}{4 π r^{5}} [3 (\vec{m} \cdot \vec{r}) \vec{r} - r^{2} \vec{m}]

Si noti la perfetta analogia con il campo elettrico generato da un dipolo elettrico.

A piccola distanza vi è una differenza sostanziale tra i campi prodotti dai dipoli elettrici e quelli magnetica, infatti, mentre il campo elettrico nello spazio tra le cariche generanti il campo dipolare si inverte, nel caso del campo magnetico, non esistendo i monopoli magnetici le linee del campo sono continue senza invertirsi.

Alcuni esercizi es. Spira, es. Dipolo ruotante, es. spira quadrata, es. disco conduttore ruotante, es. Spira con un filo, es. Dipolo magnetico e spira, precisano meglio quanto detto.

Campo di un solenoide

Il campo all'interno di un solenoide può essere calcolato generalizzando quanto detto per una spira circolare.

Un solenoide è la figura a spirale di raggio $R$ indicata in figura composta da $N$ spire su una lunghezza $L$ percorse dalla stessa corrente $I$ . Se la lunghezza fosse nulla il campo prodotto sarebbe $N$ volte quello di una singola spira.

Immaginando il solenoide avvolto in maniera uniforme. Definisco il numero di spire per unità di lunghezza come:

n = \frac{N}{L}

In un tratto $d z^{'}$ vi sono $d N = n d z^{'}$ spire che generano una corrente $d I = n I d z^{'}$ .

Poniamo l'origine delle coordinate al centro del solenoide. Il generico punto sul suo asse è $z$ mentre il generico elemento del solenoide si trova nel punto di coordinate $z^{'}$ Quindi utilizzando l'espressione trovata per una spira circolare:

d B_{z} = \frac{1}{2} μ_{o} R^{2} \frac{d I}{[R^{2} + (z^{'} - z)^{2}]^{3 / 2}} = \frac{1}{2} μ_{o} I R^{2} \frac{n d z^{'}}{[R^{2} + (z^{'} - z)^{2}]^{3 / 2}}

Integrando:

B_{z} = \frac{1}{2} μ_{o} I n R^{2} \int_{- L / 2}^{L / 2} \frac{d z^{'}}{[R^{2} + (z^{'} - z)^{2}]^{3 / 2}}

Sostituendo a $z^{'} - z = y$ , $d z^{'} = d y$ :

B_{z} = \frac{1}{2} μ_{o} I n R^{2} \int_{- L / 2 - z}^{L / 2 - z} \frac{d y}{[R^{2} + y^{2}]^{3 / 2}} = \frac{1}{2} μ_{o} I n R^{2} {[\frac{y}{R^{2} \sqrt{R^{2} + y^{2}}}]}_{- L / 2 - z}^{L / 2 - z}

B_{z} = \frac{1}{2} μ_{o} I n [\frac{L / 2 - z}{\sqrt{R^{2} + (L / 2 - z)^{2}}} + \frac{L / 2 + z}{\sqrt{R^{2} + (z + L / 2)^{2}}}]

Se $z ≪ L$ l'espressione si approssima con:

B_{z} = μ_{o} I n \frac{L}{\sqrt{4 R^{2} + L^{2}}}

che nel caso di $L ≫ R$ diventa:

B_{z} = μ_{o} n I

Mentre a grande distanza $z ≫ R, L$ il solenoide si comporta come un dipolo magnetico di momento:

\vec{m} = N I π R^{2} \hat{k}

Un solenoide ideale ha una lunghezza molto maggiore del suo diametro e le spire sono disposte in maniera compatta cioè con distanza trascurabile. In tale caso il campo è lo stesso in qualsiasi punto della sezione. Un solenoide ideale rappresenta l'equivalente magnetico del condensatore a facce piane e parallele per il campo elettrico, in quanto nel suo volume il campo magnetico è uniforme.

Azioni tra fili paralleli percorsi da corrente

Consideriamo due fili molto lunghi percorsi da correnti concordi $I_{1}$ ed $I_{2}$ posti a distanza $r$ .

Assumiamo come asse delle $z$ la direzione dei due fili e come asse delle $x$ la congiungente i due fili ed origine sul primo filo. Il primo genererà un campo pari:

\vec{B} = \frac{μ_{o}}{2 π r} I_{1} \hat{j}

Quindi (usando la regola della mano destra) sul tratto $l$ del secondo filo agirà una forza:

\vec{F} = I_{2} l \hat{k} \times \vec{B} = I_{2} l \frac{μ_{o}}{2 π r} I_{1} \hat{k} \times \hat{j} = - I_{2} l \frac{μ_{o}}{2 π r} I_{1} \hat{i}

Attrattiva nella direzione della congiungente avendo assunto che le correnti nei fili sono concordi (cioè nella stessa direzione), mentre sarà repulsiva se le correnti sono discordi. Notiamo che al contrario della legge di Coulomb, in cui cariche eguali si respingono, qui correnti nella stessa direzione si attraggono fili sono discordi (in poche parole va in maniera opposta alla forza elettrostatica di Coulomb. Come viene mostrato alla fine di questo capitolo l'effetto è spiegato dalla relatività ristretta.

La definizione di ampere è basata su tale espressione. Infatti si definisce $1 A$ quella corrente che circolando su due fili rettilinei distanti $r = 1 m$ dà luogo ad una forza di $2 \cdot 1 0^{- 7} N$ per metro.

Più in generale la forza che si esercita tra due circuiti (1 e 2), di lunghezza $L_{1}$ e $L_{2}$ vale:

\vec{F_{12}} = \frac{μ_{o} I_{1} I_{2}}{4 π} \int_{L_{1}} \int_{L_{2}} \vec{d l_{1}} \times (\frac{\vec{d l_{1}} \times \vec{r_{12}}}{r_{12}^{3}})

Campo di una carica in moto

Se consideriamo che vale l'identità:

I \vec{d l} = \vec{J} d τ

Dove $d τ$ è il volume infinitesimo di dimensione longitudinale $d l$ . La I equazione di Laplace può anche essere scritta:

\vec{d B} = \frac{μ_{\circ}}{4 π} \frac{\vec{J} \times \vec{r}}{r^{3}} d τ = \frac{μ_{\circ} n q}{4 π} \frac{\vec{v} \times \vec{r}}{r^{3}} d τ

Dove $n$ è il numero di cariche per unità di volume e quindi $d N = n d τ$ è il loro numero nel volume infinitesimo. Sostituendo anche a $μ_{\circ}$ la sua espressione in funzione di $c$ si ha che il campo di induzione magnetica generato da una singola carica (dividendo per $d N$ ) vale:

\vec{B} = \frac{1}{4 π ϵ_{o} c^{2}} q \frac{\vec{v} \times \vec{r}}{r^{3}}

Ma il campo elettrico generato da una carica puntiforme in un punto a distanza $r$ da essa vale:

\vec{E} = \frac{1}{4 π ϵ_{o}} \frac{q \vec{r}}{r^{3}}

Quindi possiamo scrivere che:

\vec{B} = \frac{1}{c^{2}} \vec{v} \times \vec{E}

In questa espressione si vede come il massimo campo che può essere generato da una carica in moto è per una carica che si muova alla velocità della luce. In ogni caso l'intensità del campo magnetico è proporzionale al rapporto $v / c^{2}$ .

Interpretazione relativistica

Se ho due cariche eguali, in moto parallelo con velocità eguale $v$ a distanza $r$ la forza elettrica vale:

\vec{F_{E}} = \frac{q^{2}}{4 π ϵ_{o}} \frac{\vec{r}}{r^{3}}

Mentre per quanto riguarda la forza dovuta al campo magnetico generato dalla prima carica sulla seconda:

\vec{F_{B}} = q \vec{v} \times (\frac{1}{4 π ϵ_{o} c^{2}} q \frac{\vec{v} \times \vec{r}}{r^{3}}) = - \frac{q^{2}}{4 π ϵ_{o}} \frac{\vec{r}}{r^{3}} \frac{v^{2}}{c^{2}}

Quindi la forza totale vale:

\vec{F} = \frac{q^{2}}{4 π ϵ_{o}} \frac{\vec{r}}{r^{3}} (1 - \frac{v^{2}}{c^{2}})

L'interpretazione secondo la relatività ristretta è logica: se mi muovo con velocità eguale a quella delle cariche, in tale sistema di riferimento le cariche sono ferme ed ho solo il campo elettrico e la forza repulsiva è quella dovuta alla forza di Coulomb; invece, in un sistema di riferimento in cui le cariche sono in moto il campo elettrico, che si propaga con la velocità della luce, parte da una carica e deve arrivare sull'altra, quindi dovendo fare un percorso maggiore arriva ridotto (rispetto al caso in cui le cariche sono ferme); al limite, in un sistema di riferimento in cui le cariche si muovono alla velocità della luce, nessuna forza elettrica arriva sull'altra, in quanto la velocità del campo elettrico è eguale a quella delle cariche. Quindi il campo magnetico è una manifestazione di un effetto puramente relativistico. Un filo percorso da corrente non genera un campo elettrico in quanto il numero della cariche negative che si muovono è pari a quello delle cariche positive; tuttavia, il moto delle cariche genera un campo magnetico (l'effetto relativistico) che invece, a causa del numero molto elevato dei portatori di carica, genera effetti macroscopici.

Il campo magnetico è in realtà un effetto relativistico che dipende sia dal sistema di riferimento che dalla limitazione della velocità della luce. Cioè se la velocità della luce fosse infinita non avrei il campo magnetico e se le cariche nel mio sistema di riferimento sono ferme non ho effetti magnetici.

Argomento seguente: Legge di Ampère

Template:Avanzamento

Fisica classica/Leggi di Laplace

Indice