Fondamenti di automatica2/Modellistica di sistemi dinamici meccanici

Rappresentazione in variabili di stato di sistemi meccanici in traslazione

Per rappresentare un sistema dinamico meccanico in termini delle variabili di stato, occorre in ordine:

1. scrivere le equazioni del moto per ogni corpo puntiforme di massa $M_i$ (eventualmente nulla) in traslazione, avente posizione $p_i$ e velocità $v_i={\dot{p}}_i$;
2. introdurre due variabili di stato per ogni corpo $M_i$ in traslazione, scegliendo in particolare la posizione $p_i$ e la velocità ${\dot{p}}_i$, in modo da trasformare ogni equazione del moto (equazione differenziale del II ordine) in una coppia di equazioni differenziali del I ordine;
3. associare una variabile di ingresso ad ogni forza esterna applicata al sistema meccanico in traslazione;
4. ricavare le equazioni di stato del tipo:

   ${\dot{x}}_i\left(t\right)=f_i(t,x\left(t\right),u\left(t\right))$

a partire dalle precedenti equazioni del moto;

5. ricavare le equazioni di uscita del tipo:

$y_k\left(t\right)=g_k(t,x\left(t\right),u\left(t\right))$

Equazioni del moto

In un sistema composto da più corpi puntiformi in traslazione, dopo aver introdotto un sistema di riferimento (assi di riferimento), per ogni corpo $M_i$ con posizione $p_i$ e velocità $v=\dot{p}$ vale la seconda legge di Newton:

$M_i{\ddot{p}}_i\left(t\right)=\sum _{{}_k}{F}_k^{\text{est}}\left(t\right)-\sum _{{}_j^{j\ne i}}{F}_{ij}^{\text{int}}\left(t\right)$

Il segno meno indica che le forze interne $F_{ij}^{\text{int}}$ trasmettono il moto agli altri corpi $M_j$, riducendo la forza d'inerzia di $M_i$.

Forze esterne

Le forze esterne $F_k^{\text{est}}$ tengono conto dell'azione del mondo esterno sul corpo $M_i$.

L'equazione generale del moto di traslazione di un corpo puntiforme di massa $M$ dovuto a forze esterne $F_i\left(t\right)$ agenti sul corpo è:

$M\ddot{p}\left(t\right)=F\left(t\right)=\sum _{{}_i}{F}_i\left(t\right)$

Le forze lungo il sistema di riferimento sono positive, mentre le forze in direzione opposta sono negative.

Forza elastica di una molla ideale di coefficiente di elasticità $K$

$F\left(t\right)=K[p_{+}\left(t\right)-p_{-}\left(t\right)]$

Forza di attrito viscoso di uno smorzatore ideale di smorzamento $\beta$

$F\left(t\right)=\beta [{\dot{p}}_{+}\left(t\right)-{\dot{p}}_{-}\left(t\right)]$

Forze interne

Le forze interne $F_{ij}^{\text{int}}$ tengono conto dell'interazione tra il corpo $M_i$ considerato e gli altri corpi $M_j$ tramite molle o smorzatori:

• molle ideali $K_{ij}$:

  $F_{ij}^{\text{int}}\left(t\right)=K_{ij}[p_i\left(t\right)-p_j\left(t\right)]$

• smorzatori ideali ${\beta }_{ij}$:

  $F_{ij}^{\text{int}}\left(t\right)={\beta }_{ij}[{\dot{p}}_i\left(t\right)-{\dot{p}}_j\left(t\right)]$

Si può modellizzare il fenomeno dell'attrito radente mediante uno smorzamento equivalente avente un'estremità fissa e lo smorzamento ${\beta }_i$ uguale al coefficiente d'attrito viscoso.

Applicazione: levitatore magnetico

Una sfera metallica di massa $M$ è tenuta sospesa dall'equilibrio tra la forza peso e la forza elettromagnetica $f\left(t\right)$ generata da un elettromagnete attraverso cui scorre una corrente $i\left(t\right)$:

$f\left(t\right)=k_i\frac{i^2\left(t\right)}{p^2\left(t\right)}$

Nella realtà basta un infinitesimo spostamento della sfera perché essa cada o venga attirata contro l'elettromagnete → serve un sistema di controllo automatico che, attraverso un trasduttore ottico di posizione, regoli la corrente $i\left(t\right)$ per bilanciare queste oscillazioni infinitesime e mantenere l'equilibrio.

Equazioni di stato

$\{\begin{array}{c}{\dot{x}}_1=x_2\\ {\dot{x}}_2=g-\frac{k_1}{M}\frac{u^2}{{x_1}^2}\end{array}$

Equazione di uscita

$y=x_1$

Rappresentazione in variabili di stato di sistemi meccanici in rotazione

Per rappresentare un sistema dinamico meccanico in termini delle variabili di stato, occorre in ordine:

1. scrivere le equazioni del moto per ogni corpo puntiforme di inerzia $J_i$ (eventualmente nulla) in rotazione, avente posizione angolare ${\theta }_i$ e velocità angolare $\omega ={\dot{\theta }}_i$;
2. introdurre due variabili di stato per ogni corpo $J_i$ in rotazione, scegliendo in particolare la posizione angolare ${\theta }_i$ e la velocità angolare ${\dot{\theta }}_i$, in modo da trasformare ogni equazione del moto (equazione differenziale del II ordine) in una coppia di equazioni differenziali del I ordine;
3. associare una variabile di ingresso ad ogni coppia esterna applicata al sistema meccanico in rotazione;
4. ricavare le equazioni di stato del tipo:

   ${\dot{x}}_i\left(t\right)=f_i(t,x\left(t\right),u\left(t\right))$

a partire dalle precedenti equazioni del moto;

5. ricavare le equazioni di uscita del tipo:

$y_k\left(t\right)=g_k(t,x\left(t\right),u\left(t\right))$

Equazioni del moto

In un sistema composto da più corpi puntiformi in rotazione, dopo aver introdotto un sistema di riferimento (versi di rotazione), per ogni corpo $J_i$ con posizione angolare ${\theta }_i$ e velocità angolare $\omega =\dot{\theta }$ vale la seconda legge di Newton:

$J_i{\ddot{\theta }}_i\left(t\right)=\sum _{{}_k}{T}_k^{\text{est}}\left(t\right)-\sum _{{}_j^{j\ne i}}{T}_{ij}^{\text{int}}\left(t\right)$

La velocità angolare $\omega =\dot{\theta }$ è rappresentata da un vettore non rotazionale determinato dalla regola della mano destra.

Il segno meno indica che le coppie interne $T_{ij}^{\text{int}}$ trasmettono il moto agli altri corpi $J_j$, riducendo la coppia d'inerzia di $J_i$.

Coppie esterne

Le coppie esterne $J_k^{\text{est}}$ tengono conto dell'azione del mondo esterno sul corpo $J_i$.

L'equazione generale del moto di rotazione di un corpo puntiforme di inerzia $J$ dovuto a coppie esterne $T_i\left(t\right)$ agenti sul corpo è:

$J\ddot{\theta }\left(t\right)=T\left(t\right)=\sum _{{}_i}{T}_i\left(t\right)$

Le coppie nel verso di rotazione concorde con il sistema di riferimento sono positive, mentre le coppie nel verso di rotazione opposto sono negative.

Coppia elastica di una molla ideale di coefficiente di elasticità torsionale $K$

$T\left(t\right)=K[{\theta }_{+}\left(t\right)-{\theta }_{-}\left(t\right)]$

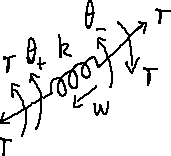
Coppia di attrito di uno smorzatore ideale di smorzamento $\beta$

$T\left(t\right)=\beta [{\dot{\theta }}_{+}\left(t\right)-{\dot{\theta }}_{-}\left(t\right)]$

Coppie interne

Le coppie interne $T_{ij}^{\text{int}}$ tengono conto dell'interazione tra il corpo $J_i$ considerato e gli altri corpi $J_j$ tramite molle o smorzatori:

• molle ideali $K_{ij}$:

  $T_{ij}^{\text{int}}\left(t\right)=K_{ij}[{\theta }_i\left(t\right)-{\theta }_j\left(t\right)]$

• smorzatori ideali ${\beta }_{ij}$:

  $T_{ij}^{\text{int}}\left(t\right)={\beta }_{ij}[{\dot{\theta }}_i\left(t\right)-{\dot{\theta }}_j\left(t\right)]$