Formulario operativo essenziale di matematica e statistica/Limite di una funzione

Il limite di una funzione per $x$ che tende a $x_0$, indicato con $\underset{x\to x_0}{lim}f(x)=L$ è il punto dell'insieme di definizione a cui tende $f(x)$ quando $x$ si "avvicina" a $x_0$. Come esempio, si guardi la figura sotto.

Limite (finito) di una funzione

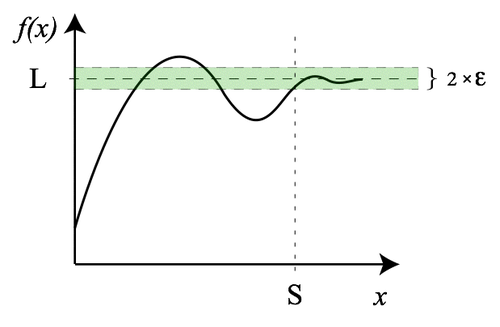
Una funzione può tendere a valori finiti o infiniti, per $x$ che tende anch'esso a valori finiti o infiniti, da sinistra (per $x\le x_0$), da destra (per $x\ge x_0$) o senza distinzione, cioè sia da destra che da sinistra. Naturalmente se $x_0=+\mathrm{\infty }$ il limite sarà sempre sinistro e viceversa.

Calcolo del valore del limite

La ricerca di $L$ varia a seconda di com'è fatta la funzione. In ogni caso, comunque, si ha che:

1. Il limite della somma di funzioni è uguale alla somma dei limiti delle singole funzioni: $\underset{x\to x_0}{lim}(f(x)+g(x))=\underset{x\to x_0}{lim}f(x)+\underset{x\to x_0}{lim}g(x)$
2. Il limite del prodotto (o del quoziente) di due funzioni è uguale al prodotto (o al quoziente) dei limiti delle singole funzioni: $\underset{x\to x_0}{lim}(f(x)\cdot g(x))=\underset{x\to x_0}{lim}f(x)\cdot \underset{x\to x_0}{lim}g(x)$
3. Il limite del prodotto di una costante per la funzione è uguale al prodotto della costante per il limite della funzione:$\underset{x\to x_0}{lim}(cf(x)),c\in ℝ=c\underset{x\to x_0}{lim}f(x)$

Limiti delle funzioni fondamentali

Tipologia di funzione	$\underset{x\to 0}{lim}$	$\underset{x\to -\mathrm{\infty }}{lim}$	$\underset{x\to +\mathrm{\infty }}{lim}$	Grafico di $f(x)$
Potenza: $x^n$, $n$ positivo	$0$	$+\mathrm{\infty }$ se $n$ è pari; $-\mathrm{\infty }$ se $n$ è dispari.	$+\mathrm{\infty }$
Funzione fratta: $\frac{1}{x^n}$, $n$ positivo	$+\mathrm{\infty }$ se $n$ è pari. Se $n$ è dispari $+\mathrm{\infty }$ a sinistra, $-\mathrm{\infty }$ a destra	$0^{+}$ se $n$ è pari, $0^{-}$ se $n$ è dispari	$0^{+}$
Costante: $c,c\in ℝ$	$c$	$c$	$c$
Esponenziale: $a^x,a>1$	$1$	$0$	$+\mathrm{\infty }$
Logaritmo: $\ln (x)$	$-\mathrm{\infty }$	$\nexists$	$+\mathrm{\infty }$
$\sin (x)$, $\cos (x)$, $\tan (x)$	$0$, $1$, $0$	$\nexists$	$\nexists$

Forme indeterminate

Rapporti di polinomi

Nel caso $lim\frac{p(x)}{q(x)}$ $\frac{\mathrm{\infty }}{\mathrm{\infty }}$ o $\frac{0}{0}$, si può tentare con la Regola di de l'Hopital:

$lim\frac{p(x)}{q(x)}=lim\frac{p^{\prime }(x)}{q^{\prime }(x)}$

sempre che $q^{\prime }(x)\ne 0,\mathrm{\forall }x$ e che tale limite esista (cioè non siano diversi tra loro quello destro e sinistro). Il procedimento è reiterabile qualora il limite trovato sia ancora in forma indeterminata.

Forme $0\cdot \mathrm{\infty }$, ${\mathrm{\infty }}^0,0^{\mathrm{\infty }}$, $0^0$

In questi casi conviene tentare di sviluppare una serie di Taylor e trasformare la funzione di cui si vuole calcolare il limite in un polinomio (quest'ultimo molto più facile da calcolare). La funzione $\sum _{n=0}^{\mathrm{\infty }}\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n$ rappresenta un'approssimazione polinomiale di grado $n$ della funzione $f(x)$ intorno al punto $x_0$. Solitamente si ricorre a Taylor per calcolare una forma indeterminata di un limite per $x\to 0$, e in tal caso la formula diventa

$\sum _{i=0}^n\frac{x^i}{i!}{f}^i(0)$

il cui calcolo del limite si spera sia semplice e non indeterminato. Solitamente ci si può fermare al grado 3.