Matematica per le superiori/Trigonometria

Misura degli Angoli

Misura in gradi sessagesimali

Il grado è la 360ª parte dell'angolo giro e a sua volta viene diviso in 60 parti, formando un primo che a sua volta può ulteriormente venire diviso in altre 60 parti, formando il secondo. Ad esempio, con 43°15'22" indichiamo un angolo di 43 gradi, 15 primi e 22 secondi.

Misura in radianti

Consideriamo un angolo α l'arco sotteso corrispondente sulla circonferenza. L'angolo misura un radiante se la lunghezza di quest'arco è uguale al raggio. Se ad esempio consideriamo un angolo arbitrario β e r il raggio, abbiamo la proporzione

$x:2\pi r={\beta }^{\circ }:360^{\circ }$

ne deriva che

$x=\frac{2\pi r{\beta }^{\circ }}{360^{\circ }}$

semplificando il tutto considerando la circonferenza goniometrica con r=1

$x=\frac{\pi {\beta }^{\circ }}{180^{\circ }}$

Si riportano qui alcuni valori in radianti dei corrispondenti gradi sessagesimali.

Gradi	0	18	30	45	60	90	135	150	180	270	360
Radianti	0	$\frac{\pi }{10}$	$\frac{\pi }{6}$	$\frac{\pi }{4}$	$\frac{\pi }{3}$	$\frac{\pi }{2}$	$\frac{3}{4}\pi$	$\frac{5}{6}\pi$	$\pi$	$\frac{3}{2}\pi$	$2\pi$

Funzioni Goniometriche

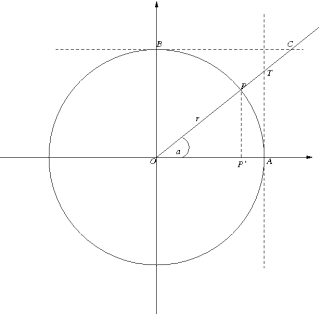
Per definire le funzioni goniometriche, consideriamo il seguente grafico, rappresentate una circonferenza goniometrica, cioè una circonferenza di equazione x²+y²=1, vale a dire una circonferenza avente raggio pari a 1.

anche se ovviamente valgono anche per qualsiasi valore del raggio.

Coseno di un angolo $\alpha$

Osservando il triangolo rettangolo POP', il coseno di un generico angolo $\alpha$ è dato dal rapporto tra il lato OP' e il raggio (nel nostro esempio 1).

$\cos \alpha =\frac{O{P}^{\prime }}{OP}=\frac{O{P}^{\prime }}{r}$

nel caso della circonferenza goniometrica, $\cos \alpha =O{P}^{\prime }$.

La funzione coseno è di tipo sinusoidale, cioè che si ripete ciclicamente. Il coseno inizia con valore 1 per l'angolo giro (o nullo), diminuendo progressivamente fino ad essere 0 quando l'angolo è 90º. Superato l'angolo retto diventa negativo assumendo -1, il suo massimo valore negativo a 180º. Superati i tali risale e diventa 0 a 270º per poi ritornare 1 raggiunti i 360º.

Seno di un angolo $\alpha$

Considerando lo stesso triangolo, il seno dell'angolo $\alpha$ è dato dal rapporto fra il segmento PP' e il raggio;

$\sin \alpha =\frac{P^{\prime }P}{OP}$

nel caso della circonferenza goniometrica di raggio=1,

$\sin \alpha =P^{\prime }P$

La funzione seno è di tipo sinusoidale. Il seno inizia con valore 0 per l'angolo giro (o nullo), aumentando progressivamente fino ad essere 1 quando l'angolo è 90º. Superato l'angolo retto si avvia a ritornare nullo, assumento nuovamente il valore 0 a 180º. Superati i tali diventa negativo e raggiunge -1 a 270º, tornando poi 0 a 360º.

Tangente e cotangente di un angolo $\alpha$

La tangente di un angolo è definita come il rapporto tra il seno ed il coseno del medesimo angolo, quindi

$\tan \alpha =\frac{\sin \alpha }{\cos \alpha }$

Possiamo dare anche un'interpretazione geometrica alla funzione tangente. Consideriamo infatti il grafico di una retta

L'equazione di questa retta è, come ben noto, $y=mx$, dove m è il coefficiente angolare. In realtà la tangente è uguale al coefficiente angolare.

Infatti, se $y=mx+q$, allora abbiamo che $m=\frac{y}{x}$ e quindi, per la definizione data all'inizio di tangente, $m=\tan \alpha$.

Osservando la circonferenza goniometrica, la tangente è il segmento AT. La tangente non può esistere quando $\alpha =\frac{\pi }{2}+k\pi$ dal momento che la retta tangente e il raggio vettore sono paralleli e non hanno quindi punti in comune.

La cotangente, come dice la seconda relazione fondamentale, è invece il reciproco della tangente:

$\cot \alpha =\frac{1}{\tan \alpha }$

Da ciò deriva che la cotangente è il rapporto tra il coseno e il seno dell'angolo e nel grafico della circonferenza goniometrica è rappresentato dal segmento BC

$\cot \alpha =\frac{\cos \alpha }{\sin \alpha }$

Il campo di esistenza della cotangente invece è$\alpha \ne k\pi \mathrm{\forall }k\in \mathbb{Z}$

A differenza del seno e del coseno, il grafico delle funzioni tangente e cotangente non formano una sinusoide, ma una tangentoide, pur essendo anch'esse cicliche. Il motivo di questa differenza risiede nel fatto che in alcuni punti la tangente non è definita, e più precisamente nei punti 90º e 270º, dove la funzione assume valori infinitamente grandi.

Il medesimo discorso vale anche per la cotangente, dove assume valore infinito nei punti 0 e 180º.

Valori delle funzioni goniometriche in alcuni angoli notevoli

Per comodità, si riportano i valori delle funzioni goniometriche in alcuni angoli notevoli.

Gradi	Radianti	seno	coseno	tangente	cotangente
0	0	0	1	0	$\varnothing$
15º	$\frac{1}{12}\pi$	$\frac{\sqrt{6}-\sqrt{2}}{4}$	$\frac{\sqrt{6}+\sqrt{2}}{4}$	$2-\sqrt{3}$	$2+\sqrt{3}$
18º	$\frac{\pi }{10}$	$\frac{\sqrt{5}-1}{4}$	$\frac{\sqrt{10+2\sqrt{5}}}{4}$	$\sqrt{\frac{5-2\sqrt{5}}{5}}$	$\sqrt{5+2\sqrt{5}}$
30º	$\frac{\pi }{6}$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{3}}{3}$	$\sqrt{3}$
45º	$\frac{\pi }{4}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{2}}{2}$	1	1
60º	$\frac{\pi }{3}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$	$\frac{\sqrt{3}}{3}$
75º	$\frac{5}{12}\pi$	$\frac{\sqrt{6}+\sqrt{2}}{4}$	$\frac{\sqrt{6}-\sqrt{2}}{4}$	$2+\sqrt{3}$	$2-\sqrt{3}$
90º	$\frac{\pi }{2}$	1	0	$\varnothing$	0

Con l'uso di questi valori e con le formule che vedremo in seguito, è possibile calcolare il valore delle funzioni anche oltre i 90º combinandole in vari modi.

Archi Associati

Abbiamo già visto che il seno ed il coseno assumono valori da -1 a 1 ciclicamente (ovviamente sempre nel caso della circonferenza goniometrica di raggio 1). In questa sezione vediamo come il seno ed il coseno si ripetono e si scambiano al variare dell'angolo e dei quadranti, rendendo quindi così possibile ridurre tutti i valori delle due funzioni al primo quadrante.

Angoli Complementari

Consideriamo l'angolo $\alpha$ e l'angolo $\frac{\pi }{2}-\alpha$;

I due triangoli OHP e OH'P' sono uguali (essendo gli angoli uguali) e uguali sono i loro lati, ovvero seno e coseno. Allora: $\frac{\sin (\frac{\pi }{2}-\alpha )}{\cos (\frac{\pi }{2}-\alpha )}=\frac{\cos \alpha }{\sin \alpha }=\cot \alpha$

Angoli Supplementari

Consideriamo ora l'angolo $\alpha$ e l'angolo $\pi -\alpha$;

Anche in questo caso i triangoli sono uguali (OHP e OH'P' hanno il medesimo angolo $\alpha$), e osservando la figura si deduce che

$\sin (\pi -\alpha )=\sin \alpha$

$\cos (\pi -\alpha )=-\cos \alpha$

$\tan (\pi -\alpha )=\frac{-\sin \alpha }{\cos \alpha }=-\tan \alpha$

Se invece consideriamo l'angolo $\frac{\pi }{2}+\alpha$, otteniamo un angolo che differisce di un angolo retto da $\alpha$ e la relazione tra seno e coseno è identica a quella di $\pi -\alpha$ e $\alpha$.

Sono due modi di vedere lo stesso angolo, come ad esempio, possiamo vedere un angolo di 110º sia come 180º-70º sia come 90º+20º.

Angoli che hanno per somma tre angoli retti

Consideriamo l'angolo $\frac{3\pi }{2}-\alpha$ e $\alpha$;

Anche in questo caso i triangoli sono uguali e osservando la figura si deduce che

$H^{\prime }{P}^{\prime }=-HP\Rightarrow \cos (\frac{3\pi }{2}-\alpha )=-\sin \alpha$

$O{H}^{\prime }=-OH\Rightarrow \sin (\frac{3\pi }{2}-\alpha )=-\cos \alpha$

$\tan (\frac{3\pi }{2}-\alpha )=\cot \alpha$

$\cot (\frac{3\pi }{2}-\alpha )=\tan \alpha$

Possiamo anche vedere la situazione come angoli che differiscono di un angolo piatto, ed in tal caso considerare $\pi +\alpha$ e $\alpha$ e arrivare ai precedenti risultati nel medesimo modo, ossia osservando il grafico.

Angoli esplementari

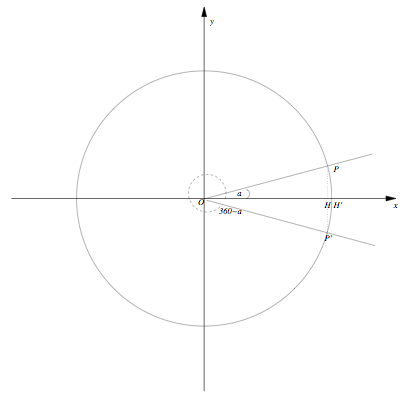
Consideriamo la differenza tra l'angolo giro e un angolo $\alpha$, ossia $2\pi -\alpha$;

Al solito, anche questi triangoli sono uguali e possiamo notare che

$H^{\prime }{P}^{\prime }=-HP\Rightarrow \sin (2\pi -\alpha )=-\sin \alpha$

$O{H}^{\prime }=OH\Rightarrow \cos (2\pi -\alpha )=\cos \alpha$

$\tan (2\pi -\alpha )=-\tan \alpha$

$\cot (2\pi -\alpha )=-\cot \alpha$

Anche qui possiamo vedere le cose in modo diverso, ossia sommando un angolo $\alpha$ a 270°, facendo però attenzione perché il risultato è diverso.

Infatti, osservando il grafico

abbiamo che

$H^{\prime }{P}^{\prime }=HP\Rightarrow \cos (\frac{3\pi }{2}+\alpha )=\sin \alpha$

$O{H}^{\prime }=-OH\Rightarrow \sin (\frac{3\pi }{2}+\alpha )=-\cos \alpha$

$\tan (\frac{3\pi }{2}+\alpha )=-\cot \alpha$

$\cot (\frac{3\pi }{2}+\alpha )=-\tan \alpha$

Angoli opposti

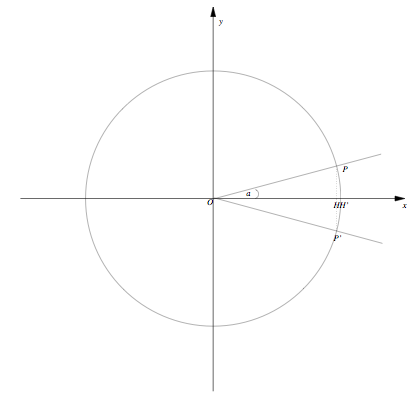
Infine consideriamo due angoli opposti $\alpha$ e $-\alpha$, ovvero l'angolo $360^{\circ }-\alpha$;

Ovviamente i trinagoli sono uguali e abbiamo che:

$H^{\prime }{P}^{\prime }=-HP\Rightarrow \sin (2\pi -\alpha )=-\sin \alpha$

$O{H}^{\prime }=OH\Rightarrow \cos (2\pi -\alpha )=\cos \alpha$

$\tan (2\pi -\alpha )=-\tan \alpha$

$\cot (2\pi -\alpha )=-\cot \alpha$

Operazioni algebriche con le funzioni goniometriche

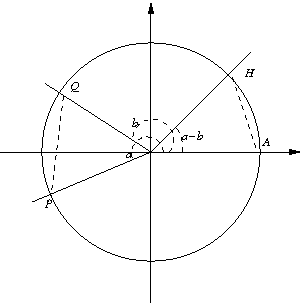
Osserviamo la figura, dove vengono rappresentati un angolo $\alpha$, $\beta$ e la loro differenza $\alpha -\beta$:

Con le funzioni goniometriche abbiamo che

$\sin (\alpha +\beta )\ne \sin \alpha +\sin \beta$

e per rendersene conto è sufficiente un semplice esempio: $\alpha =\beta =30^{\circ }$ il cui seno vale $\frac{1}{2}$. È ovvio che $\sin 60^{\circ }\ne \sin 30^{\circ }+\sin 30^{\circ }$ perché i rispettivi risultati sono $\frac{\sqrt{3}}{2}$ e 1.

Per avere il coseno e il seno dell'angolo $\alpha -\beta$, è necessario utilizzare delle formule fondamentali da ricordare.

Formule di Sottrazione e Addizione

Queste formule permettono di ottenere il seno e il coseno di una somma algebrica di due angoli tramite il seno e il coseno dei singoli addendi. Non mi metto a scrivere tutti i calcoli che bisogna fare per arrivare a queste formule (potete ad esempio trovarli nella pagina http://ripmat.it/mate/i/ic/icaaa.html), mi limito a scrivere le formule cosicché puoi memorizzarle e consultarle velocemente.

$\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta$

$\sin (\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta$

$\cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$

$\cos (\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta$

Riguardo tangente e cotangente:

$\tan (\alpha +\beta )=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }$

$\tan (\alpha -\beta )=\frac{\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }$

$\cot (\alpha +\beta )=\frac{\cot \alpha \cot \beta -1}{\cot \beta +\cot \alpha }$

$\cot (\alpha -\beta )=\frac{\cot \alpha \cot \beta +1}{\cot \beta -\cot \alpha }$

Formule di Duplicazione

Sono formule che derivano dalle formule precedenti, ponendo $\alpha =\beta$.

Il motivo di queste formule deriva dal fatto che in generale:

$2\sin \alpha \ne \sin 2\alpha$

$2\cos \alpha \ne \cos 2\alpha$ ecc...

Valgono allora le seguenti formule che permettono di ottenere il seno, coseno, tangente e cotangente dell'angolo doppio rispetto a quello dato.

$\sin 2\alpha =2\sin \alpha \cos \alpha$

$\cos 2\alpha =\{\begin{array}{c}{\cos }^2\alpha -{\sin }^2\alpha \\ 1-2{\sin }^2\alpha \\ 2{\cos }^2\alpha -1\end{array}$

$\tan 2\alpha =\frac{2\tan \alpha }{1-{\tan }^2\alpha },\alpha \ne \pi +2k\pi \wedge \alpha \ne \frac{\pi }{4}+k\frac{\pi }{2}$

$\cot 2\alpha =\frac{{\cot }^2\alpha -1}{2\cot \alpha },\alpha \ne k\frac{\pi }{2}$

Formule di Bisezione

Le formule di bisezione consentono di ottenere il seno, coseno, tangente e cotangente della metà di un generico angolo $\alpha$, avendo il coseno di $\alpha$.

$\sin \frac{\alpha }{2}=\pm \sqrt{\frac{1-\cos \alpha }{2}}\{\begin{array}{c}+se\frac{\alpha }{2}IoIIquadrante\\ -se\frac{\alpha }{2}IIIoIVquadrante\end{array}$

$\cos \frac{\alpha }{2}=\pm \sqrt{\frac{1+\cos \alpha }{2}}\{\begin{array}{c}+se\frac{\alpha }{2}IoIVquadrante\\ -se\frac{\alpha }{2}IIoIIIquadrante\end{array}$

$\tan \frac{\alpha }{2}=\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }}\{\begin{array}{c}+se\frac{\alpha }{2}IoIIIquadrante\\ -se\frac{\alpha }{2}IIoIVquadrante\end{array}$

$\cot \frac{\alpha }{2}=\pm \sqrt{\frac{1+\cos \alpha }{1-\cos \alpha }}\{\begin{array}{c}+se\frac{\alpha }{2}IoIVquadrante\\ -se\frac{\alpha }{2}IIoIIIquadrante\end{array}$

Formule di Prostaferesi

Le formule di prostaferesi permettono di trasformare una somma o sottrazione di seni, coseni, ecc... in un prodotto.

$\sin \alpha +\sin \beta =2\sin \frac{\alpha +\beta }{2}\cos \frac{\alpha -\beta }{2}$

$\sin \alpha -\sin \beta =2\sin \frac{\alpha -\beta }{2}\cos \frac{\alpha +\beta }{2}$

$\cos \alpha -\cos \beta =-2\sin \frac{\alpha +\beta }{2}\sin \frac{\alpha -\beta }{2}$

$\tan \alpha \pm \tan \beta =\frac{\sin (\alpha \pm \beta )}{\cos \alpha \cos \beta },\alpha ,\beta \ne \frac{(2k+1)\pi }{2}$

$\cot \alpha \pm \cot \beta =\frac{\sin (\beta \pm \alpha )}{\sin \alpha \sin \beta },\alpha ,\beta \ne k\pi$

Formule di Werner

Queste formule sono un po' l'inverso delle formule di prostaferesi, ovvero le formule di Werner consentono di trasformare il prodotto di due seni, coseni o un prodotto di seno per un coseno, nelle rispettive somme o differenze.

$\sin \alpha \sin \beta =\frac{1}{2}[\cos (\alpha -\beta )-\cos (\alpha +\beta )]$

$\cos \alpha \cos \beta =\frac{1}{2}[\cos (\alpha +\beta )+\cos (\alpha -\beta )]$

$\sin \alpha \cos \beta =\frac{1}{2}[\sin (\alpha +\beta )+\sin (\alpha -\beta )]$

Formule parametriche

Le formule parametriche consentono di ricavare seno, coseno e cotangente mediante la tangente dell'angolo metà.

$\sin \alpha =\frac{2\tan \frac{\alpha }{2}}{1+{\tan }^2\frac{\alpha }{2}}$

$\cos \alpha =\frac{1-{\tan }^2\frac{\alpha }{2}}{1+{\tan }^2\frac{\alpha }{2}}$

$\tan \alpha =\frac{2\tan \frac{\alpha }{2}}{1-{\tan }^2\frac{\alpha }{2}}$

$\cot \alpha =\frac{1-{\tan }^2\frac{\alpha }{2}}{2\tan \frac{\alpha }{2}}$

Torna al sommario