Fisica classica/Induzione e legge di Faraday

Template:Capitolo Template:Fisica classica Questa legge ha rappresentato la vera svolta dell'elettromagnetismo nello sviluppo della società industriale e indica il legame forte esistente tra campi elettrici e magnetici. Per descriverla con compiutezza bisogna fare delle premesse basate su quanto già detto in precedenza.

Il flusso di induzione magnetica attraverso una qualsiasi superficie chiusa è sempre eguale a zero, in quanto non vi sono monopoli magnetici. Possiamo quindi considerare una qualsiasi linea chiusa dello spazio e associare ad essa una superficie che abbia tale linea come contorno, il flusso attraverso tale superficie è lo stesso qualsiasi superficie si consideri. Un circuito composto da $N$ spire ha come contorno una linea chiusa dello spazio, ma in realtà il flusso del campo di induzione magnetica è $N$ volte il flusso associato alla linea chiusa considerato: tale flusso viene chiamato flusso concatenato al circuito considerato.

Si deve a Faraday nel 1831 la scoperta che se si ha una variazione nel tempo del flusso magnetico concatenato con un circuito ${\mathrm{\Phi }}_B$ si ha una f.e.m. secondo la relazione algebrica:

$f.e.m.=-\frac{d{\mathrm{\Phi }}_B}{dt}$.

Nel seguito precisiamo il significato di questa legge di valore fondamentale. Il segno meno il cui significato è spiegato nella cosiddetta legge di Lenz verrà precisato nel seguito.

Vari esempi possono essere dati per illustrare quando si verifica una condizione di questo tipo. Tradizionalmente si possono raggruppare i vari casi possibili in varie categorie:

Due circuiti accoppiati senza parti in movimento

Esperimento di Faraday con due circuiti accoppiati senza parti in movimento

Viene riprodotto uno degli esperimenti originali di Faraday in forma schematica, una batteria alimenta il circuito di sinistra generando una corrente variabile nel tempo. Il circuito di destra ben accoppiato, avvolto sullo stesso toro magnetico, è attraversato da una corrente elettrica, che viene misurata dal galvanometro, un strumento che misura la corrente elettrica. Quando nel circuito di sinistra la corrente diviene stazionaria, nessuna corrente viene più misurata dal galvanometro. La corrente circolante nel circuito di destra dipende dalla variazione della corrente in quello di sinistra, cioè tende a contrastare o l'aumento del flusso magnetico concatenato o la diminuzione, questo è evidenziato dal segno della corrente misurata nel galvanometro. In questo che in questo caso non si abbia niente in moto e quindi la legge di Faraday rappresenta una assoluta novità, rispetto a leggi precedenti.

Nell'esempio di un solenoide con una spira viene chiarito questo caso generale.

Un circuito fisso in un campo magnetico in moto

Esperimento di Faraday con due circuiti accoppiati con una corrente stazionaria nella bobina A (in moto) accoppiata ad una bobina più grande B (fissa) che ha in serie un galvanometro G, a sinistra

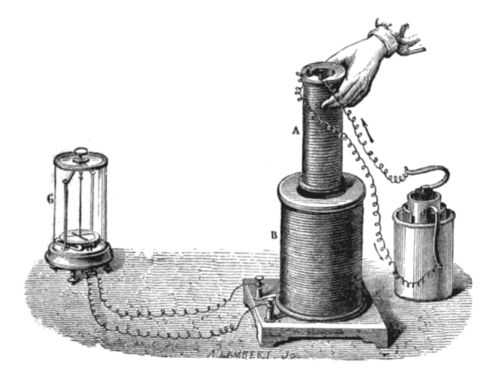
Immaginiamo di avere una piccola bobina A alimentata da un generatore di f.e.m. e accoppiata ad una bobina maggiore B che ha in serie un galavanometro G. Se il circuito A è fermo nessuna corrente viene misurata dal galavanometro. Mentre se viene mosso come mostrato in figura si genera una f.e.m. misurata dal galvanometro, con un verso tale da contrastare la variazione del flusso concatenato.

Il caso più banale è quello che la bobine siano solenoidali. Quando il bordo del solenoide A attraversa la sezione del solenoide B il flusso concatenato nel solenoide B aumenta e viene indotta una corrente nel solenoide B che contrasta l'aumento del campo. L'ampiezza della corrente indotta dipende dalla velocità e dalla posizione relativa. Infine quando il bordo riattraversa la sezione del solenoide B il flusso concatenato nel solenoide B diminuisce e si genera una corrente di segno opposto al caso precedente nel solenoide B per contrastare tale variazione del flusso. La stessa cosa si ottiene con un magnete permanente, che genera un campo non uniforme, che si muova rispetto ad una bobina.

Il fatto che il moto sia rettilineo non ha nessuna rilevanza, infatti la stessa cosa l'avremmo anche nel caso di sorgente in moto rotatorio, anzi in questo caso anche una sorgente che sia uniforme spazialmente genererà nella bobina una f.e.m. indotta.

L' esempio di una spira in un campo magnetico ruotante chiarisce quanto detto.

Un circuito in moto in un campo magnetico fisso

Immaginiamo di avere una sorgente fissa di campo magnetico ed un circuito che si muova rispetto al campo non uniforme. Il moto del circuito lo supponiamo per semplificare la cosa, rettilineo e uniforme. Come si vede è il caso simmetrico rispetto a quello indicato prima: ma dal punto di vista della meccanica classica del tutto equivalente. Infatti entrambi i sistemi sono inerziali e chi si muove rispetto all'altro non cambia. In ogni caso in questo caso la forza di Lorentz giustifica l'apparire di una f.e.m.

Supponiamo il circuito quadrato di lato $a$ ed il campo perpendicolare al piano del circuito in moto con due lati paralleli alla direzione del moto. Nei due lati perpendicolari alla direzione del moto si genererà una f.e.m. opposta ma non eguale, a causa della uniformità del campo di induzione magnetica. Tale differenza è la causa della f.e.m. indotta.

Analogamente, nell'esempio di una spira in un campo magnetico ruotante se facciamo ruotare la spira invece del campo, le equazioni rimangono le stesse come il risultato finale, solo che in questo caso la legge di Faraday si identifica con la Forza di Lorentz. In realtà che un circuito si muova in un campo fisso, o il circuito si muova in un campo fisso rappresentano lo stesso fenomeno ed è la causa di un fenomeno vistoso.

Correnti parassite

Correnti parassite (I, rosso) indotte in una piastra metallica (C) in movimento verso destra di un magnete stazionario (N). Il campo magnetico (B, verde) è diretto verso il basso. Le correnti generano il proprio campo magnetico (frecce blu) che produce una forza di resistenza che si oppone al moto.

Le correnti parassite sono causate dal movimento di un conduttore in un campo magnetico. Il moto relativo genera nel conduttore una corrente che può essere anche molto intensa, e quindi produce a sua volta un campo magnetico che tende come vedremo a rallentare la variazione del campo magnetico .

La corrente che si sviluppa nel conduttore ha una forma vorticosa perché gli elettroni sono soggetti alla Forza di Lorentz che è perpendicolare alla direzione degli elettroni stessi in movimento. Quindi, essi ruotano alla loro destra, o sinistra, a seconda del senso del campo applicato e della variazione del campo in aumento o in diminuzione. La resistività del conduttore smorza queste correnti.

Le correnti parassite generano perdite di energia riscaldando il conduttore per effetto Joule.

I forni ad induzione e i freni magnetici (quelli usati nei treni, sono un esempio dell'applicazioni di tale effetto. Questo fenomeno in molte applicazioni risulta negativo ad esempio nei trasformatori e nei motori elettrici determina una diminuzione dell'efficienza. Le perdite avvengono nei nuclei che in questi dispositivi sono conduttori. Si possono attenuare queste perdite scegliendo un nucleo magnetico che abbia una bassa conducibilità elettrica (ad esempio: ferriti, acciaio al silicio) o suddividendo il nucleo magnetico in sottili strati, elettricamente isolati.

Un circuito di dimensioni variabili in un campo magnetico

A causa del fatto che uno o più lati del circuito si muovano, si ha che sulle cariche libere di tali lati agisce la forza di Lorentz mutuamente perpendicolare sia al campo che alla direzione del moto; tale forza genera una f.e.m.. Quindi anche in questo caso la legge di Faraday non aggiunge niente rispetto alle leggi del magnetismo. Ma è più facile anche in questo caso trattare il problema, senza fare distinzioni, mediante la legge di Faraday. Questo approccio è seguito nell'esercizio di una sbarretta metallica.

Legge di Lenz

Il verso delle correnti indotte è tale da generare un campo magnetico che si oppone alla variazione del flusso del campo magnetico concatenato con il circuito. Tale legge giustifica fisicamente il segno meno che compare nella legge di Faraday. Infatti la f.e.m. indotta dalla variazione del flusso concatenato è tale da opporsi alla causa che lo ha generato, in maniera che se il flusso magnetico esterno aumenta la corrente circolante tende a rallentare tale incremento, mentre se diminuisce la corrente circolante tende a lasciare immutato il campo magnetico iniziale.

La legge è ovviamente in accordo con la conservazione dell'energia, se infatti la legge fosse per assurdo di segno opposto, una piccola variazione del flusso concatenato produrrebbe una maggiore variazione con un effetto moltiplicativo che violerebbe la conservazione dell'energia.

L'alternatore

Questa è la più importante applicazione della legge di Faraday per lo sviluppo della società industriale . Supponiamo di avere una bobina quadrata realizzata con $N$ spire (i ragionamenti in realtà non dipendono dalla forma, ma per semplificazione usiamo la forma quadrata) ed un campo magnetico ruotante (rotore) come in figura.

Schema di un semplice alternatore con un campo magnetico ruotante (rotore) e una spira fissa (statore), viene anche mostrato la corrente indotta nello statore dal campo magnetico ruotante del rotore.

A causa della rotazione del campo magnetico il flusso attraverso la bobina varierà in funzione del tempo. Quindi ai capi della bobina si genererà una f.e.m. Se l'area della bobina è $S$, e $\theta$ l'angolo compreso tra la normale ($\overrightarrow{n}$) alla bobina e la direzione del campo di induzione magnetica ($\overrightarrow{B}$), il flusso di induzione magnetica concatenato con le $N$ spire della bobina vale:

${\mathrm{\Phi }}_c(B)=N\overrightarrow{B}\cdot \overrightarrow{S}=N|B|S\cos \theta$

Se mediante un qualsiasi mezzo propulsivo il rotore viene mantenuto in rotazione con velocità angolare $\omega$ costante allora:

$\theta =\omega t$

Applicando la legge di Faraday:

$f.e.m=N|B|S\omega \sin \omega t$

Cioè ai capi della bobina vi è una d.d.p. che varia con legge sinusoidale nel tempo: questo dispositivo si chiama alternatore o generatore di corrente alternata. Se l'attrito è trascurabile l'energia meccanica utilizzata per mantenere in rotazione a velocità angolare fissa viene integralmente trasformata in energia elettrica dissipata dal carico (un eventuale elemento dissipativo posto ai suoi estremi). Quindi l'alternatore rappresenta il metodo più usato per trasformare energia meccanica in energia elettrica, in corrente alternata, che è comoda da trasportare su grandi distanze. La corrente che circola nel carico (immaginando che sia una semplice resistenza $R$) è semplicemente eguale a:

$I=\frac{N|B|S\omega }{R}\sin \omega t$

L'alternatore di una automobile con la cinghia metallica trascina il rotore

Nel fare tale ragionamento si è trascurata una proprietà della bobina che viene definita nel seguito: la sua induttanza.

Studiamo il bilancio energetico di un sistema di questo genera che produce istantaneamente una potenza elettrica pari a:

$P_e=f.e.m.I=\frac{N^2{B}^2{S}^2}{R}{\omega }^2{\sin }^2\omega t$

Dal punto di vista meccanico sulla spira a causa del fatto che la spira è un dipolo magnetico immerso in un campo magnetico:

$|\overrightarrow{m}|=NIS$

Su di esso agisce una coppia di momento pari a:

$\overrightarrow{M}=\overrightarrow{m}\times \overrightarrow{B}$

Che in questo caso specifico, proiettandolo sull'asse $z$ di rotazione, vale:

$M_z=NIBS\sin \omega t$

La potenza meccanica necessaria a mantenere in rotazione a velocità angolare costante un corpo rigido su cui agisce una coppia è pari secondo la meccanica dei corpi rigidi:

$P_m=M_z\omega$

Sostituendo l'espressione di $I$ in $M_z$ segue che:

$P_m=\frac{N^2{B}^2{S}^2}{R}{\omega }^2{\sin }^2\omega t$

Cioè in assenza di attrito tutta l'energia meccanica viene trasferita in energia elettrica. Le centrali elettriche ma anche semplicemente i generatori interni delle automobili producono energia elettrica mediante tale meccanismo di conversione diretta di energia meccanica in energia elettrica. La figura invece mostra l'alternatore tipico di una automobile che trasforma l'energia meccanica in tutta l'utenza elettrica di una automobile, ricaricando le batterie.

Induttanza

Il flusso concatenato con un circuito e la corrente che in esso circola sono direttamente proporzionali: la costante di proporzionalità viene chiamata induttanza del circuito:

$L=\frac{{\mathrm{\Phi }}_c(B)}{I}$

Il simbolo di una induttanza

'E una grandezza puramente geometrica connessa con l'area racchiusa da un circuito ed il campo magnetico generato nel complesso quando in detto circuito scorre una corrente elettrica. Il simbolo dell'induttanza è mostrato di lato. Le dimensioni fisiche dell'induttanza sono quelle del rapporto tra un flusso magnetico e una corrente, nel SI si misura in Henry ($H$)

$[L]=\frac{[B][l^2]}{[I]}=[T][m{]}^2[A{]}^{-1}=[H]$

Il simbolo ricorda vagamente la forma di un solenoide, e in particolare nel caso di solenoidi sufficientemente lunghi e compatti, è facile calcolare l'induttanza. Infatti essendo il flusso concatenato di un solenoide di lunghezza $l$, di raggio $r$ e con $N$ spire, in cui scorre una corrente $I$:

${\mathrm{\Phi }}_c(B)=N{\mu }_{\circ }\frac{N}{l}I\pi r^2$

quindi:

$L_{solenoide}={\mu }_{\circ }\frac{N^2}{l}\pi r^2$

Il calcolo dell'induttanza per circuiti abbastanza semplici non è in genere facile. Come regola generale se il circuito è fatto di $N$ spire che si sovrappongono bene l'induttanza cresce con $N^2$. Quindi per bobine semplici di superficie $S$ semplice l'induttanza è circa eguale a:

$L\approx {\mu }_{\circ }{N}^2\sqrt{S}$

La presenza di materiali ferromagnetici aumenta l'induttanza di molti ordini di grandezza: è facile costruire induttanze di molti Henry.

A partire da queste considerazioni, la permeabilità magnetica del vuoto, di cui avevamo dato le dimensioni fisiche a partire dalla formula del campo di induzione magnetica prodotta da un filo rettilineo, può esprimersi in funzione della unità scelta per la induttanza .nel sistema SI divengono adesso:

${\mu }_{\circ }=4\pi \times 10^{-7}H/m$

Per geometrie semplici l'induttanza cresce linearmente con le dimensioni lineari e per spire estremamente vicine con il quadrato del numero delle spire.

Mutua induttanza

Simbolo della mutua induttanza di due circuiti, n ed m sono il numero di spire del primario e secondario, mentre i punti indicano che le bobine sono avvolte in maniera concorde

Dati due circuiti chiaramente il flusso magnetico dell'uno si concatenerà con l'altro. Il rapporto tra il flusso concatenato su di uno e la corrente che scorre sull'altro viene chiamata mutua induzione.

$M=M_{12}=\frac{{\mathrm{\Phi }}_{c1}}{I_2}=M_{21}=\frac{{\mathrm{\Phi }}_{c2}}{I_1}$

Notiamo come la mutua induzione gode della proprietà di reciprocità, cioè la mutua induzione di un primo circuito rispetto ad un secondo è pari alla mutua induzione del secondo sul primo.

La dimostrazione si può fare in maniera rigorosa ma richiede di richiamare il collegamento con il potenziale vettore:
$M_{12}=\frac{1}{I_1}\underset{S2}{\int }{\overrightarrow{B}}_1\cdot \overrightarrow{d{S}_2}=\frac{1}{I_1}\underset{S2}{\int }\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{A_1}\cdot \overrightarrow{d{S}_2}$
Per il teorema di Stokes, definendo con $l_2$ la linea che costituisce il contorno di $S_2$:
$\underset{S2}{\int }\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{A_1}\cdot \overrightarrow{d{S}_2}={\oint }_{l_2}{\overrightarrow{A}}_1\cdot \overrightarrow{d{l}_2}$
Quindi:
$M_{12}=\frac{1}{I_1}{\oint }_{l_2}\overrightarrow{A_1}\cdot \overrightarrow{d{l}_2}$
Se chiamiamo $l_1$ la linea che costituisce il contorno di $S_1$:
$\overrightarrow{A_1}=\frac{{\mu }_o}{4\pi }{I}_1{\oint }_{l_1}\frac{\overrightarrow{d{l}_1}}{|r_{12}|}$
Quindi:
$M_{12}=\frac{{\mu }_o}{4\pi }{\oint }_{l_1}{\oint }_{l_2}\frac{\overrightarrow{d{1}_1}\cdot \overrightarrow{d{l}_2}}{|r_{12}|}$
Ripetendo l'analogo ragionamento per $M_{21}$:
$M_{21}=\frac{{\mu }_o}{4\pi }{\oint }_{l_2}{\oint }_{l_1}\frac{\overrightarrow{d{1}_2}\cdot \overrightarrow{d{l}_1}}{|r_{21}|}$
Poiché il prodotto scalare come l'integrale di linea non dipendono dall'ordine dei fattori, la mutua induzione tra due circuiti è una grandezza geemetrica unica.
Numericamente il calcolo della mutua induzione viene fatto utilizzando la formula data per calcolare la reciprocità tra $M_{12}$ ed $M_{21}$
Ma anche l'induttanza di un circuito è calcolabile numericamente con una espressione simile:
$L=\frac{{\mu }_o}{4\pi }{\oint }_{l_1}{\oint }_{l_1}\frac{\overrightarrow{d{1}_1}\cdot \overrightarrow{d{l}_2}}{|r_{21}|}$

A causa quindi della reciprocità si ha che:

$M=M_{12}=M_{21}$

A partire dalla definizione analitica si ha anche che:

$M=k\sqrt{L_1{L}_2}$

Definendo $0\le k\le 1$ la costante di accoppiamento tra i due circuiti.

Due esempi: Mutua induzione tra due spire quadrate, Due spire possono aiutare a capire i concetti espressi.

Cenno sui trasformatori

Schema di principio di un toro di materiale ferromagnetico con due avvolgimenti: un tipico trasformatore

Simbolo circuitale del trasformatore

In un toro di materiale ferromagnetico di sezione costante $S$ e lunghezza media $l$ con permeabilità magnetica ${\mu }_r$ su cui sono avvolte $N$ spire tutto il flusso rimane confinato nell'interno del toro ed utilizzando il teorema della circuitazione di Ampere, si trova che il campo di induzione magnetica vale all'interno del toro:

$B={\mu }_o{\mu }_r\frac{NI}{l}$

e di conseguenza l'induttanza vale:

$L={\mu }_o{\mu }_r{N}^2\frac{S}{l}$

Se i circuiti avvolti sono due con $N_1$ ed $N_2$ spire, l'accoppiamento tra i circuiti è il massimo possibile e di conseguenza la mutua induzione vale:

$M={\mu }_o{\mu }_r{N}_1{N}_2\frac{S}{l}$

I circuiti di questo tipo sono alla base di quelli che vengono chiamati i trasformatori. Il trasformatore ha un interesse importante in e per questa ragione vengono descritti con maggiore dettaglio nel prossimo capitolo

Transitori induttivi

Iniezione di corrente da un generatore di f.e.m. su una induttanza

L'introduzione dell'induttanza ci permette di calcolare la f.e.m. indotta da variazioni di flusso concatenate con circuiti percorsi da corrente elettrica variabile nel tempo. Immaginiamo di avere un generatore di f.e.m che viene connesso ad una resistenza in serie con una induttanza mediante l'interruttore mostrato in figura. La legge di Faraday si riduce nel caso di una induttanza all'espressione:

$f_a=-\frac{d{\mathrm{\Phi }}_c(B)}{dt}=-L\frac{dI}{dt}$

Dove il pedice $a$ sta a indicare che si tratta di forza elettromotrice autoindotta che tende a impedire le variazioni di correnti al suo interno.

Nel caso specifico abbiamo introdotto una resistenza $R$ in serie che tiene conto della eventuale resistenza interna del generatore, dell'induttanza (sono entrambe in serie) o una resistenza esterna.

L'equazione della maglia nel tempo del circuito deve tenere conto che agisce non solo il generatore di forza elettromotrice $f$, ma anche la forza elettromotrice autoindotta $f_a$:

$f+f_a=RI$

Sostituendo i vari termini:

$RI=f-L\frac{dI}{dt}$

da cui separando le variabili

$\frac{dI}{I-f/R}=-\frac{R}{L}dt$

definendo $\tau =L/R$, e integrando tra il tempo $t=0$ in cui la corrente è nulla ed il tempo generico segue che:

$\ln \frac{I(t)-f/R}{-f/R}=-\frac{t}{\tau }$

che diventa:

$I=\frac{f}{R}(1-e^{-t/\tau })$

Iniezione di corrente da un generatore di f.e.m. su una induttanza con in parallelo una resistenza grande

Il significato della equazione è che a causa della $f_a$ in un circuito la corrente non raggiunge istantaneamente il valore $f/R$, ma si avvicina asintoticamente con una costante di tempo $L/R$.

Il termine $-L\frac{dI}{dt}$ dovuto alla legge di Faraday, viene nella maggior parte dei casi considerato una ulteriore d.d.p. e quindi aggiunta con il segno opposto dall'altro lato della equazione. Questo approccio verrà seguito nel seguito, anche se porta a qualche contraddizione.

Per far vedere il caso opposto, e rendere l'esempio fisicamente credibile dobbiamo considerare un caso sostanzialmente simile a quello descritto illustrato nella figura a fianco. Immaginiamo grande la resistenza in parallelo all'induttanza (questo significa $\alpha \gg 1$. Secondo questa ipotesi il sistema non è molto differente dal precedente, infatti ai capi dell'induttanza il circuito è equivalente utilizzando il Teorema di Thevenin, e considerando che $\alpha \gg 1$ a:

$R_{th}=R\frac{\alpha }{\alpha +1}\approx R$

$f_{th}=f\frac{\alpha }{\alpha +1}\approx f$

Quindi se partiamo dalla condizione iniziale illustrata con l'interruttore chiuso (avendo aspettato un tempo sufficientemente lungo), la corrente che inizialmente scorre nell'induttanza diviene:

$I_o\approx \frac{f}{R}$

Mentre la d.d.p. ai capi di $\alpha R$ sarà nulla.

Se a questo punto apriamo l'interruttore avremo la seguente equazione che descrive la maglia:

$-L\frac{dI}{dt}=\alpha RI$

da cui separando le variabili

$\frac{dI}{I}=-\frac{\alpha R}{L}dt$

Se ora definiamo $\tau =\frac{L}{\alpha R}$ ed integriamo (cambiando il nome delle variabili):

$\underset{I_o}{\overset{I}{\int }}\frac{d{I}^{\prime }}{I^{\prime }}=-\underset{0}{\overset{t}{\int }}\frac{d{t}^{\prime }}{\tau }$

Da cui:

$I(t)=I_o{e}^{-t/\tau }$

La tensione ai capi della resistenza (di polarità opposta a quando è collegato al generatore di f.e.m. diventa:

$V(t)=I_o\alpha R{e}^{-t/\tau }\approx \alpha f{e}^{-t/\tau }$

Alcuni esempi permettono di comprendere quanto detto: induttanza e due resistenze, induttanza e tre resistenze, spira tonda e solenoide

Energia magnetica

Il fenomeno della iniezione di corrente su una induttanza con una resistenza in serie da parte di un generatore di f.e.m. possiamo esaminarlo dal punto di vista del generatore riscrivendo l'equazione del transitori vista precedentemente come:

$f=RI+L\frac{dI}{dt}$

Moltiplicando tutti i termini per la corrente che istantaneamente scorre nella maglia:

$fI=R{I}^2+LI\frac{dI}{dt}$

Quindi integrando nel tempo i vari termini:

$\underset{0}{\overset{t}{\int }}fId{t}^{\prime }=\underset{0}{\overset{t}{\int }}R{I}^{2}d{t}^{\prime }+\underset{0}{\overset{t}{\int }}LI\frac{dI}{dt}d{t}^{\prime }$

$\underset{0}{\overset{t}{\int }}fId{t}^{\prime }=\underset{0}{\overset{t}{\int }}R{I}^{2}d{t}^{\prime }+L\underset{0}{\overset{I}{\int }}L{I}^{\prime }d{I}^{\prime }$

abbiamo da una parte l'energia totale formata dal generatore e dall'altra due termini, il primo l'energia dissipata per effetto Joule nella resistenza e il secondo:

$E_L=L\underset{0}{\overset{I}{\int }}L{I}^{\prime }d{I}^{\prime }=\frac{1}{2}L{I}^2$

è un termine che qui viene definito per la prima volta l'energia immagazzinata nell'induttanza. Tale energia viene accumulata sotto forma di energia magnetica, come si può far vedere nel caso più generale. Consideriamo due casi: un solenoide ideale, un toro di materiale ferromagnetico

Solenoide

In un solenoide molto lungo e compatto l'induttanza vale:

$L=N^2{\mu }_o\frac{\pi r^2}{l}$

Dove $N$ è il numero di spire, $r$ il raggio, ed $l$ la lunghezza.

$E_L=\frac{1}{2}{N}^2{\mu }_o\frac{\pi r^2}{l}{I}^2$

Ma in un solenoide:

$B={\mu }_o\frac{N}{l}I$

Per cui si può riscrivere l'equazione precedente come:

$E_L=\frac{1}{2{\mu }_o}{B}^{2}l\pi r^2$

Ma $l\pi r^2$ è il volume racchiuso dal solenoide in cui il campo magnetico è costante, quindi l'energia immagazzinata nel campo magnetico per unità di volume vale:

$u_M=\frac{1}{2{\mu }_o}{B}^2$

Un toro ferromagnetico

Una induttanza costituita N spire e in cui scorre una corrente $I$ avvolte su un toro ferromagnetico di sezione costante il più semplice circuito magnetico. Chiamiamo $\ell$ la lunghezza media del perimetro del toro ed $S$ la sua sezione. Le direzioni di $\overrightarrow{H}$ e $\overrightarrow{B}$ sono dovunque le stesse e quindi possiamo definire una permeaibilità relativa ${\mu }_r$, che dipenderà dalla corrente $I$ e dalla storia del materiale ma che possiamo definire dalla relazione:

$\overrightarrow{B}={\mu }_0{\mu }_r\overrightarrow{H}$

L'induttanza della bobina in questo caso è:

$L={\mu }_0{\mu }_r\frac{N^{2}S}{\ell }$

Ma anche:

$|H|=\frac{NI}{\ell }|B|={\mu }_0{\mu }_r\frac{NI}{\ell }$

Quindi l'energia magnetica:

$E_L=\frac{1}{2}{\mu }_0{\mu }_r\frac{N^{2}S}{\ell }{I}^2=\frac{1}{2}\frac{NI}{\ell }{\mu }_0{\mu }_r\frac{NI}{\ell }S\ell =\frac{1}{2}|H||B|S\ell$

L'energia immagazzinata nel campo magnetico per unità di volume vale quindi:

$u_M=\frac{1}{2}HB$

Pressione magnetica

L'energia per unità di volume del campo magnetico è eguale alla pressione che tende a deformare le strutture che generano i campi magnetici. In quanto campi magnetici molto intensi tendono a fare esplodere i magneti e l'effetto è molto importante per i grandi magneti. Notiamo che vi è una differenza sostanziale con i campi elettrici che al contrario tendono a fare implodere le strutture, in quanto cariche di segno opposto come quelle tra le armature di un condensatore tendono ad attrarsi. Nel caso dei magneti si ha esattamente l'effetto opposto in quanto i lati paralleli di una bobina essendo percorsi da corrente di segno opposto si respingono. La pressione magnetica è pari a:

$P_M=\frac{1}{2{\mu }_o}{B}^2$

Esempio:
Quindi se vogliamo fare un campo di induzione magnetica di 10 T è necessario impedire la esplosione della bobina che lo genera in quanto  la
pressione che deve sopportare la struttura è di:
$P_M=\frac{1}{2{\mu }_o}{B}^2\approx 8\cdot 10^{7}Pa$
cioè circa 800 Atmosfere. 
Tanto per fare un confronto anche tra le armature di un condensatore a facce piane e parallele vi è una pressione (che  però tende a fare implodere la struttura), ma anche se ho campo elettrico molto intenso ad esempio di 107 V/m la pressione tra le armature è di solo
$P_E=\frac{{\epsilon }_o}{2}{E}^2\approx 4.4\cdot 10^{2}Pa$
cioè 200 volte meno della pressione atmosferica.

Argomento seguente: Correnti alternate

Template:Avanzamento