Controlli automatici/Sistemi di controllo digitali

Sistema di controllo digitale

Schema base di un sistema di controllo digitale

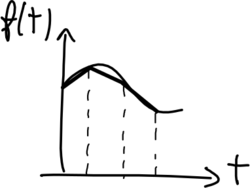
Campionatore

Il campionatore è un convertitore A/D che genera in uscita la sequenza di campioni $\left\{e_k\right\}$ con passo di campionamento $T$ a partire dall'errore di inseguimento $e(t)$:

• nel dominio del tempo:

  $e^{*}(t)=e(t)\sum _{k=0}^{+\mathrm{\infty }}\delta (t-kT)=\sum _{k=0}^{+\mathrm{\infty }}{e}_k\cdot \delta (t-kT)$

• nel dominio della trasformata zeta:

  $𝒵\left\{\left\{e_k\right\}\right\}=E^{*}\left(z\right)=\sum _{k=0}^{+\mathrm{\infty }}{e}_k\cdot z^{-k}$

• nel dominio della trasformata di Laplace:

  $ℒ\left\{e^{*}\left(t\right)\right\}=E^{*}(s)=\sum _{k=0}^{+\mathrm{\infty }}{e}_k\cdot e^{-kTs}={E^{*}(z)|}_{z=e^{sT}}$

Il passo di campionamento $T$ deve essere sufficientemente piccolo:

• il teorema del campionamento impone una pulsazione di campionamento ${\omega }_s$ maggiore del doppio della pulsazione di banda ${\omega }_B$:

  ${\omega }_s\gg {\omega }_B$

• la riduzione del margine di fase $m_{\phi }$ introdotta dal ricostruttore deve essere contenuta:

  ${\omega }_s\gg {\omega }_c$

Il passo di campionamento $T$ non deve essere troppo piccolo, per non incorrere in:

• problemi di quantizzazione;
• necessità di utilizzare processori costosi per garantire elevate prestazioni.

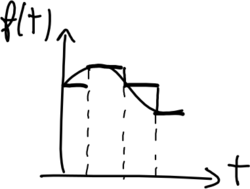
Ricostruttore

Ricostruzione del segnale tramite un filtro Z.O.H.

Il ricostruttore è un convertitore D/A che genera il comando $u(t)$ a partire dalla sua sequenza di campioni $\left\{u_k\right\}$. Il filtro Template:Tooltip di ordine zero mantiene nell'intervallo $T$ il comando $u(t)$ pari al valore dell'ultimo campione acquisito. La funzione di trasferimento del filtro Z.O.H. si può approssimare a una funzione razionale tramite l'approssimazione di Padè del I ordine:

$H_0(s)=\frac{U(s)}{U^{*}(s)}=\frac{1-e^{-sT}}{s}\cong \frac{T}{1+s\frac{T}{2}}$

La funzione di trasferimento $H_0(s)$ del filtro Z.O.H. ha un polo in $-\frac{2}{T}$ che crea una perdita di fase in corrispondenza della pulsazione di taglio ${\omega }_c$, cioè una riduzione del margine di fase $m_{\phi }$. Riducendo via via il passo di campionamento $T$, il polo si sposta ad una pulsazione sufficientemente elevata rispetto alla pulsazione di taglio ${\omega }_c$ con conseguente riduzione della perdita del margine di fase $m_{\phi }$.

Controllore digitale

Il controllore digitale è definito dalla sua funzione di trasferimento $C(z)$ nel dominio della trasformata zeta, che è calcolabile tramite un metodo di discretizzazione a partire dalla funzione $C(s)$ del controllore analogico.

Metodi di approssimazione dell'integrazione nel tempo

• 
  Metodo delle differenze all'indietro
• 
  Metodo delle differenze in avanti
• 
  Trasformazione bilineare o di Tustin

• metodo delle differenze all'indietro: approssima mantenendo costante l'ultimo campione:

  metodo non valido: genera forti distorsioni

• metodo delle differenze in avanti: approssima mantenendo costante il prossimo campione:

  metodo non valido: non garantisce la stabilità di $C(z)$ ottenuta a partire da $C(s)$ stabile

• trasformazione bilineare (o di Tustin): approssima tramite trapezi:

  metodo valido: genera distorsioni ridotte, e garantisce la stabilità di $C(z)$ ottenuta a partire da $C(s)$ stabile

• trasformazione bilineare con precompensazione in frequenza: precalcola e compensa la distorsione alla pulsazione di taglio ${\omega }_c$:

  metodo valido: genera distorsioni molto ridotte, e garantisce la stabilità di $C(z)$ ottenuta a partire da $C(s)$ stabile

Altri metodi

• metodo di invarianza della risposta all'impulso: garantisce che a fronte di un medesimo ingresso ad impulso la sequenza di campioni all'uscita di $C(z)$ coincida con la sequenza di valori assunti negli istanti di campionamento dall'uscita di $C(s)$:

  metodo non valido: non garantisce l'assenza di aliasing

• metodo di invarianza della risposta al gradino: garantisce che a fronte di un medesimo ingresso a gradino la sequenza di campioni all'uscita di $C(z)$ coincida con la sequenza di valori assunti negli istanti di campionamento dall'uscita di $C(s)$, ed è equivalente a considerare $C(s)$ in cascata a un fittizio filtro Z.O.H.:

metodo valido: garantisce l'assenza di aliasing

• metodo della corrispondenza poli-zeri: calcola direttamente i poli e gli zeri di $C(z)$ a partire da quelli di $C(s)$ ($z=e^{sT}$):

  metodo valido

Progetto per la realizzazione del controllore digitale

1. si sceglie il passo di campionamento $T$:
   • si considera come prima scelta un valore dell'ordine di qualche millisecondo:

     $T=\frac{2\pi }{\alpha {\omega }_B},5\le \alpha \le 20$

   • si valuta il nuovo margine di fase $m_{\phi }$ della funzione d'anello corrispondente alla cascata del campionatore, del controllore e del filtro Z.O.H. approssimato (basta introdurre il termine $1+s\frac{T}{2}$ a denominatore della funzione d'anello del sistema da controllare);
   • se il margine di fase $m_{\phi }$ risulta insufficiente, si riduce il passo di campionamento $T$ per quanto possibile;
2. si sceglie un metodo di discretizzazione e si calcola la funzione $C(z)$ del controllore digitale a partire da $C(s)$;
3. si verifica il comportamento del sistema complessivo in presenza del controllore digitale $C(z)$:
   • analisi a tempo discreto (in frequenza e nel tempo): si trasformano in zeta la funzione d'anello $G_a(s)$ e la funzione di trasferimento in catena chiusa $W_y(s)$ del sistema, scegliendo il metodo di invarianza della risposta al gradino come metodo per trasformare la funzione $F(s)$ del sistema da controllare;
   • simulazione del sistema ibrido con Simulink.