Fisica classica/Dinamica del corpo rigido

Definizione di corpo rigido

Una rappresentazione grafica dei 3 angoli che caratterizzano un corpo rigido

Un sistema di punti che mantengano fissa la loro distanza reciproca viene chiamato corpo rigido; ovviamente questa è sempre una semplificazione per permetterci di trattare alcune caratteristiche del moto di un corpo. In quanto la perfetta indeformabilità di un corpo non è possibile, sicuramente l'approssimazione è molto buona per alcuni tipi di oggetti compatti fatti di materiali come l'acciaio, vetro, l'alluminio, ma anche il legno, non certamente oggetti in gomma o in metalli morbidi come l'indio che non possono considerarsi rigidi.

La descrizione completa della dinamica di un corpo rigido è possibile se si conosce la posizione nello spazio di un suo generico punto (in genere si sceglie il centro di massa) e di tre angoli come mostrato nella figura a fianco. La posizione del centro di massa, anche se il centro di massa è al di fuori del corpo, è immutabile nel tempo rispetto agli altri punti del corpo rigido, quindi in genere per determinare il moto di un corpo rigido si studia la traiettoria del centro di massa e di un asse di riferimento inerziale con origine sul centro di massa.

Non variando le distanze tra i punti la risultante delle forze interne al sistema sono nulle come anche il loro momento, per cui le equazioni cardinali della meccanica si riducono a:

$\overrightarrow{R}=M{\overrightarrow{a}}_{CM}$

(1)

$\overrightarrow{\tau }=\frac{d\overrightarrow{L}}{dt}$

(2)

Abbiamo omesso l'apice ext che è pleonastico poiché solo le forze e i momenti esterni possono variare lo stato di moto di un corpo rigido. Inoltre per quanto riguarda l'energia cinetica solo il lavoro $W$ delle forze e dei momenti delle forze esterne può provocare una variazione della energia cinetica del corpo:

$\mathrm{\Delta }{E}_k=W$

(3)

Il moto di un corpo rigido può essere molto complicato in quanto nel caso generale tutte e sei le grandezze fisiche che lo descrivono (la posizione del centro di massa e i tre angoli) possono variare nel tempo e nello spazio. Vi sono due casi particolari più semplici che è possibile considerare per semplificare la trattazione: il moto traslatorio ed il moto rotatorio.

Moto traslatorio

Movimento puramente traslazionale di un corpo rigido

Esaminiamo il caso di un moto solo traslatorio. In questo caso tutti i punti del corpo rigido descrivono traiettorie eguali come nella figura a fianco, quindi la velocità di ogni singolo punto del corpo coincide istante per istante con la velocità del centro di massa. Il moto è descritto in maniera analoga a quanto avviene per un punto materiale. Le grandezze fisiche di maggiore interesse sono l'energia cinetica e la quantità di moto totale del sistema. La dinamica del corpo è determinata da solamente la prima equazione cardinale della dinamica.

$\overrightarrow{R}=M{\overrightarrow{a}}_{CM}$

La quantità di moto totale del sistema $\overrightarrow{P}=M{\overrightarrow{v}}_{CM}$ e il momento angolare totale rispetto ad un polo che dista ${\overrightarrow{r}}_{CM}$ dal centro di massa sono grandezze collegate. Infatti si mostra che dal primo teorema di König il momento angolare rispetto a tale asse si riduce:

$\overline{L}={\overrightarrow{r}}_{CM}\times \overrightarrow{P}$

Ma $\overrightarrow{P}$ è la quantità di moto del sistema che dipende dalla sola prima equazione cardinale della meccanica. Quindi la seconda equazione cardinale:

$\overrightarrow{\tau }=\frac{d\overrightarrow{L}}{dt}={\overrightarrow{r}}_{CM}\times \frac{d\overrightarrow{P}}{dt}={\overrightarrow{r}}_{CM}\times \overrightarrow{R}$

non aggiunge alcuna informazione alla conoscenza della dinamica del corpo rigido, se il moto è puramente traslatorio.

Moto rotatorio

Movimento puramente rotatorio di un'asta attorno al punto O

Esaminiamo il caso di un moto rotatorio attorno ad un asse fisso. In questo caso tutte le parti del corpo compiono delle orbite circolari attorno all'asse di rotazione e quindi si muovono con velocità istantanea tanto maggiore quanto sono distanti dall'asse di rotazione. Nella figura a fianco muovendosi l'asta con velocità angolare $\overrightarrow{\omega }$ (senso antiorario, verso uscente dal piano di rotazione), la velocità dei singoli punti distanti $\overrightarrow{R}$ da O, valgono $\overrightarrow{\omega }\times \overrightarrow{R}$. Se la velocità angolare è costante il moto dei singolo punti è circolare uniforme. Se la velocità angolare varia nel tempo vi debbono essere momenti delle forze esterne che causano tale moto rotatorio vario e la seconda equazione cardinale è l'unica necessaria a descrivere il moto:

$\frac{d\overrightarrow{L}}{dt}=\overrightarrow{\tau }$

Se il centro di massa si trova sull'asse di rotazione essendo nulla la accelerazione del centro di massa:

${\overrightarrow{a}}_{CM}=0$

la prima equazione cardinale è identicamente nulla. Ma anche se il centro di massa non si trova sull'asse di rotazione, come nella figura, il suo moto sarà una orbita circolare esattamente con tutti gli altri elementi, e quindi in media la forza risultante sarà nulla, quindi la prima equazione cardinale non aggiunge nulla alle informazioni della seconda equazione cardinale.

Convenzioni nel moto rotatorio dei corpi rigidi

Se la rotazione avviene attorno ad un asse fisso del corpo rigido nell'intervallo di tempo $dt$ si avrà una rotazione di un angolo $d\theta$: viene convenzionalmente definito un vettore $\overrightarrow{d}\theta$, che ha come modulo l'angolo e come direzione l'asse di rotazione (se il senso è antiorario). Quindi una regione del corpo rigido, identificata dal vettore $\overrightarrow{r}$ che congiunge l'asse di rotazione e la regione, si sposta durante la rotazione di un arco $\overrightarrow{d}s$:

$\overrightarrow{d}s=\overrightarrow{d}\theta \times \overrightarrow{r}$

Di conseguenza poiché la direzione dell'asse di rotazione non cambia nel tempo, anche la velocità istantanea del punto rimane tangente alla traiettoria circolare:

$\overrightarrow{v}=\frac{\overrightarrow{d}s}{dt}=\frac{\overrightarrow{d}\theta }{dt}\times \overrightarrow{r}=\overrightarrow{\omega }\times \overrightarrow{r}$

Se la velocità angolare non è costante l'accelerazione tangenziale vale:

${\overrightarrow{a}}_t=\frac{d\overrightarrow{v}}{dt}=\frac{d\overrightarrow{\omega }}{dt}\times \overrightarrow{r}=\overrightarrow{\alpha }\times \overrightarrow{r}$

L'accelerazione centripeta a causa della rigidità del corpo non ha un ruolo nella dinamica del sistema. Notiamo come i tre vettori $\overrightarrow{d}\theta$, $\overrightarrow{\omega }$ ed $\overrightarrow{\alpha }$ siano paralleli all'asse di rotazione e concordi con esso se il moto è antiorario.

Moto rototraslatorio

Esempio di moto rototraslatorio una sfera su una superficie con A il punto di contatto. Il punto A ha una velocità molto inferiore alle altre e non è rappresentata.

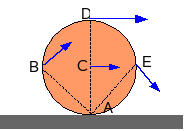
Il moto traslatorio ed il moto rotatorio attorno ad un asse fisso sono descrivibili in maniera semplice. Ma il caso più generale è quello di un moto in cui contemporaneamente vi sia traslazione e rotazione attorno ad un asse che cambia nel tempo. Questo è il caso più generale che senza perdere di generalità può essere descritto per spostamenti infinitesimi. In cui si ha contemporaneamente una traslazione infinitesima e un rotazione infinitesima caratterizzate da una velocità istantanea $\overrightarrow{v}$ ed una velocità angolare istantanea $\overrightarrow{\omega }$.

La descrizione di un generico moto di un sistema rigido non è univoca. La figura è un esempio. Potrebbe essere una boccia lanciata su una superficie nel moto iniziale. Il punto di contatto con il suolo A trasla e contemporaneamente a causa della forza di attrito la sfera ruota attorno al punto di contatto. Vedremo nel seguito che dopo un certo tempo aumenta la rotazione e diminuisce la traslazione ed il punto di contatto è istantanamente fermo questo è il moto di puro rotolamento, che studieremo in seguito. Qui stiamo studiando un caso diverso in cui A si muove, ma le velocità dei due punti A,B,C,D,E sono diverse come appare dalla figura, ma concentriamo l'attenzione sulla velocità dei punti C e D rispetto ad A:

${\overrightarrow{v}}_D={\overrightarrow{v}}_A+\overrightarrow{\omega }\times \overrightarrow{AD}$

${\overrightarrow{v}}_C={\overrightarrow{v}}_A+\overrightarrow{\omega }\times \overrightarrow{AC}$

Sottraendo membro a membro le due espressioni precedenti si ha che:

${\overrightarrow{v}}_D-{\overrightarrow{v}}_C=\overrightarrow{\omega }\times (\overrightarrow{AD}-\overrightarrow{AC})$

${\overrightarrow{v}}_D={\overrightarrow{v}}_C+\overrightarrow{\omega }\times \overrightarrow{CD}$

In questa maniera si è messo in relazione la velocità di D non più rispetto ad A, ma rispetto a C che è il nuovo polo. In questa operazione matematica appare evidente che, mentre la velocità istantanea del punto D dipende dal polo scelto per la rotazione, è infatti diversa da quella rispetto al punto A, il valore della velocità angolare istantanea non dipende dalla scelta fatta. Quindi nel caso generale del moto rototraslatorio mentre la parte traslazionale dipende dalla scelta del polo considerato per studiare la dinamica la velocità angolare non dipende da tale scelta. Quindi nella fotografia istantanea $\overrightarrow{\omega }$ è definità in maniera univoca: ma nel caso generale può cambiare nel tempo di direzione e verso.

Centro di massa di un corpo rigido

Un corpo rigido si rappresenta in maniera più semplice, non come un insieme di punti materiali come appare nella sua natura microscopica (essendo costituito da un insieme di atomi), ma come un mezzo continuo caratterizzato dalla sua densità:

$\rho (\overrightarrow{r})=\frac{dm}{dV}$

Cioè la densità è il rapporto tra la massa infinitesima (dm) ed il volume (dV) da essa occupata. La densità è una grandezza che dipende dalla posizione e viene definita non solo per i corpi rigidi. La massa totale m di un corpo rigido di volume V vale:

$M=\underset{V}{\int }\rho (\overrightarrow{r})dV$

(4)

Se la densità non varia all'interno del corpo, cioè $\rho (\overrightarrow{r})=costante$, il corpo si dice omogeneo. In questo caso:

$M=\rho V$

Nel sistema internazionale la densità si misura in kg/m³, anche se è più comune l'uso nel linguaggio comune dell'unità di misura del sistema cgs, cioè il g/cm³. La definizione di densità vale sia per i solidi come i fluidi.

La densità dell'acqua è alla temperatura di  4 oC circa 1 g/cm3 o 1000 kg/m3, tra gli elementi l'Osmio 
(un metallo nobile simile al Platino) ha la massima densità 22.66 g/cm3. 

Nei corpi unidimensionali (corde, tubi) si introduce il concetto di densità lineare definita come:

$\lambda =\frac{dm}{dl}$

dove dl è l'elemento infinitesimo di linea.

Due esempi su corpi unidimensionali:mezzo anello e quarto di anello possono chiarire i concetti.

Nei corpi bidimensionali (superfici) si definisce la densità superficiale come:

$\sigma =\frac{dm}{dS}$

dove dS è l'elemento infinitesimo di superficie.

Il centro di massa di un generico corpo rigido si ottiene per estensione della definizione data di centro di massa per un insieme discreto di punti:

${\overrightarrow{r}}_{CM}=\frac{\sum _{i=1}^n{m}_i{\overrightarrow{r}}_i}{\sum _{i=1}^n{m}_i}=\frac{\sum _{i=1}^n{m}_i{\overrightarrow{r}}_i}{m}$

sostituendo alla sommatoria l'integrale:

${\overrightarrow{r}}_{CM}=\frac{\underset{V}{\int }\overrightarrow{r}\rho (\overrightarrow{r})dV}{m}$

(5)

Nei corpi omogenei e dotati di simmetria attorno ad un punto, il centro di massa coincide con il punto stesso, analogamente se vi è un asse (piano) di simmetria il centro di massa è sull'asse (piano) stesso. Il centro di massa coincide con il centro della forza peso: il baricentro. Il baricentro dipende dalla forza peso e quindi è definito per i corpi si trovano sulla superficie della terra.

Alcuni esempi chiariscono meglio:mezzo disco e mezza sfera, quarto di disco e sfera con foro la posizione del centro di massa di oggetti non simmetrici.

Moto rotatorio

Mentre il moto traslatorio di un corpo rigido è una semplice generalizzazione del moto di un punto materiale. Il moto rotatorio presenta delle peculiarità per quanto riguarda il momento angolare e l'evoluzione del moto. Il momento angolare di un insieme di punti materiali vale:

$\overrightarrow{L}=\sum _{i=1}^n{\overrightarrow{r}}_i\times {\overrightarrow{m}}_i{\overrightarrow{v}}_i$

La sua espressione nel caso continuo è:

$\overrightarrow{L}=\int \overrightarrow{r}\times \overrightarrow{v}dm$

Per studiare la dinamica, anche nel caso di semplice rotazione, bisogna introdurre una nuova grandezza fisica: il momento di inerzia. Un caso semplice elementare serve da introduzione al problema.

Esempio di un guscio cilindrico

Un cilindro sottile.

Consideriamo un sottile guscio cilindrico di massa M e raggio R (di spessore trascurabile rispetto ad R) che ruota con velocità angolare $\overrightarrow{\omega }$ attorno ad un asse passante per il centro e perpendicolare al piano del cilindro stesso. In questo caso è facile calcolare il momento angolare totale. Essendo tutti i punti del corpo rigido alla stessa distanza dal centro di rotazione, R, la loro velocità è pari in modulo a $v=\omega R$, quindi il momento angolare totale vale semplicemente:

$\overrightarrow{L}=M{R}^2\overrightarrow{\omega }$

Cioè è proporzionale ad $\overrightarrow{\omega }$ con una grandezza caratteristica del guscio stesso relativa all'asse di rotazione scelto, detto il momento di Inerzia $I=M{R}^2$. Un guscio sottile se l'altezza è trascurabile diventa un anello sottile (spesso il caso più elementare trattato è quello di un anello).

Momento di Inerzia

Dato un generico corpo rigido che ruota intorno ad un asse la relazione tra la velocità e la velocità angolare $v=\omega r$ rimane valida, anche se $r$ non è una costante, come nel caso del guscio cilindrico, ma dipende dalla distanza del generico elemento del corpo dall'asse di rotazione.

Come estensione del caso precedente definiamo momento di inerzia di un corpo rigido la grandezza scalare:

$I=\underset{V}{\int }{r}^{2}dm$

(6)

dove r è la distanza dall'asse delle masse infinitesime dm di cui si compone il compone il corpo di volume V.

Il momento di inerzia in tutti i corpi rigidi ha la dimensione di una massa per una distanza al quadrato, è una proprietà geometrica del corpo che dipende dall'asse attorno a cui avviene la rotazione, che nel caso della rotazione dei corpi rigidi ha una funzione simile alla massa nel caso di moto traslatorio. Il momento di inerzia è uno scalare, anche se dipende dall'asse attorno a cui viene calcolato. Essendo definito come integrale di grandezze scalari $r^2$ e $dm$ gode della proprietà di additività, se calcolato attorno lo stesso asse: cioè se ho un solido complesso posso calcolarmi il momento di inerzia separatamente per le varie parti del corpo rispetto allo stesso asse e poi sommare i vari termini. L'importanza del momento di inerzia appare nella dinamica del moto rotatorio come vedremo nel seguito.

Moto rotatorio con asse fisso di simmetria

Nel caso particolare di $\overrightarrow{L}$ parallelo a $\overrightarrow{\omega }$, cioè quando l'asse attorno a cui avviene la rotazione è un asse di simmetria del corpo. La definizione di asse di simmetria da un punto di vista concettuale è data nel seguito. Se è applicato un momento di una forza $\overrightarrow{\tau }$ rispetto all'asse di rotazione il momento angolare $\overrightarrow{L}$ varia e il collegamento tra variazione del momento angolare e momento della forza è dato dalla seconda equazione cardinale della dinamica:

$\overrightarrow{\tau }=\frac{d\overrightarrow{L}}{dt}=I\frac{d\overrightarrow{\omega }}{dt}=I\overrightarrow{\alpha }$

(7)

Dove $\overrightarrow{\alpha }$ è la derivata della velocità angolare anche essa parallela all'asse di rotazione. Vi è quindi una notevole analogia in questo caso tra la II equazione della dinamica ($\overrightarrow{F}=m\overrightarrow{a}$ ), infatti la massa inerziale rappresenta la resistenza alla variazione della traslazione di un corpo, mentre il momento di inerzia è la resistenza alla variazione nel moto rotatorio. Ma bisogna aggiungere che, seppure il momento di inerzia sia una proprietà geometrica, essa dipende dall'asse di rotazione.

Legge oraria

Se $\overrightarrow{\tau }=0$ si ha che:

$\alpha =0$

Quindi, la velocità angolare è costante o nulla:

$\omega ={\omega }_o$

Quindi il corpo rigido si muove di moto circolare uniforme attorno all'asse di rotazione:

$\theta ={\theta }_o+{\omega }_{o}t$

Se $\overrightarrow{\tau }=costante$ allora anche la accelerazione angolare è costante:

$\alpha ={\alpha }_o$

$\omega ={\omega }_o+{\alpha }_{o}t$

$\theta ={\theta }_o+{\omega }_{o}t+\frac{1}{2}{\alpha }_o{t}^2$

(8)

Se $\overrightarrow{\tau }$ è variabile, anche il moto circolare è variabile e la soluzione è diversa da questa.

Momenti di inerzia

Asta rigida

Un'asta rigida con un asse passante per il centro.

Un caso molto semplice è quello di Asta di lunghezza L e massa M attorno ad un asse passante per il suo centro di massa e perpendicolare alla direzione dell'asta, è facile mostrare come utilizzando la densità lineare:

$\lambda =\frac{M}{L}$

Estendendo la definizione di momento di inerzia (il fatto di potere fare una integrazione presuppone l'additività del momento di inerzia):

$I_c=\underset{-L/2}{\overset{L/2}{\int }}{r}^2\lambda dr=\lambda {\left[\frac{r^3}{3}\right]}_{-L/2}^{L/2}$

Un'asta rigida con un asse passante per estremo.

Da cui si ha che il momento di inerzia vale:

$I_C=\frac{M{L}^2}{12}$

Se invece come nella figura a destra l'asse passa per un estremo si ha che:

$I_e=\underset{0}{\overset{L}{\int }}{r}^2\lambda dr=\lambda {\left[\frac{r^3}{3}\right]}_0^L$

$I_e=\frac{M{L}^2}{3}$

Disco sottile

Disco sottile.

Un disco sottile omogeneo di raggio r e massa m ha una densità superficiale di:

$\sigma =\frac{M}{\pi r^2}$

nel calcolo del momento di inerzia si può considerarlo come è un insieme di anelli di raggio $0\le R\le r$ e quindi di superficie $dS=2\pi RdR$, la cui massa vale

$dm=\sigma 2\pi RdR$.

Quindi il momento di inerzia per l'asse di simmetria (come in figura) vale:

$I=\underset{0}{\overset{r}{\int }}{R}^2\sigma 2\pi RdR=2\pi \sigma \underset{0}{\overset{r}{\int }}{R}^{3}dR=\pi \sigma \frac{r^4}{2}$

$I=\frac{1}{2}M{r}^2$

Guscio sferico

Guscio sferico

Un guscio omogeneo di raggio r e massa M ha una densità superficiale di:

$\sigma =\frac{M}{4\pi r^2}$

A causa della simmetria sferica ogni asse passante per il centro è equivalente. Quindi scegliamo un asse qualunque passante per il centro come asse $z$ attorno a cui vogliamo calcolare il momento di inerzia. Possiamo ridurre il singolo elemento infinitesimo ad un anello di raggio $R$, che dipende dall'angolo $\theta$ tra $r$ e $z$:

$R=r\sin \theta con0\le \theta \le \pi$

La cui superficie vale:

$dS=2\pi Rrd\theta =2\pi r^2\sin \theta d\theta$

Quindi la cui massa vale:

$dm=2\pi r^2\sin \theta d\theta \sigma =\frac{M}{2}\sin \theta d\theta$

$d{I}_z=\frac{M}{2}\sin \theta d\theta R^2=\frac{M}{2}{r}^2{\sin }^3\theta d\theta$

$I_z=\frac{M}{2}{r}^2\underset{0}{\overset{\pi }{\int }}{\sin }^3\theta d\theta =\frac{M}{2}{r}^2{[-\cos \theta +{\cos }^3\theta /3]}_0^{\pi }=\frac{2}{3}M{r}^2$

Sfera

Sfera

Una sfera omogenea di raggio r e massa M ha una densità di:

$\rho =\frac{3M}{4\pi r^3}$

A causa della simmetria sferica ogni asse passante per il centro è equivalente. Quindi scegliamo un asse qualunque passante per il centro come asse $z$ attorno a cui vogliamo calcolare il momento di inerzia. Possiamo ridurre il singolo elemento infinitesimo ad un guscio sferico $0\le R\le r$ e spessore $dR$ il cui volume vale:

$dV=4\pi R^{2}dR$

Quindi di massa:

$dm=\rho dV=\frac{3M}{4\pi r^3}4\pi R^{2}dR=\frac{3M}{r^3}{R}^{2}dR$

Quindi utilizzando la formula del guscio sferico, ha un momento di inerzia (infinitesimo) pari a:

$d{I}_z=\frac{2}{3}dm{R}^2=\frac{2}{3}\frac{3M}{r^3}{R}^{4}dR=\frac{2M}{r^3}{R}^{4}dR$

Quindi il momento d'inerzia totale di una sfera piena vale:

$I_z=\underset{0}{\overset{r}{\int }}d{I}_z=\frac{2M}{r^3}\underset{0}{\overset{r}{\int }}{R}^{4}dR=\frac{2}{5}M{r}^2$

Alcuni momenti di inerzia

Per tutte le figure semplici è possibile calcolare il momento di inerzia. La tabella seguente riassume il valore di alcuni momenti di inerzia per alcuni solidi.

Descrizione	Figura	Momenti di inerzia
Due punti materiali M e m, con massa ridotta μ e a distanza, x.		$I=\frac{Mm}{M+m}{x}^2=\mu x^2$
Asta rigida di lunghezza L, massa M, spessore trascurabile, con asse ad un estremo .		$I_{\mathrm{e}\mathrm{n}\mathrm{d}}=\frac{M{L}^2}{3}$
Asta rigida di lunghezza L, massa M, spessore trascurabile, con asse al centro .		$I_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}=\frac{M{L}^2}{12}$
Anello di raggio r e massa M di spessore trascurabile.		$I_z=M{r}^2$ $I_x=I_y=\frac{M{r}^2}{2}$
Disco di raggio r e massa M.		$I_z=\frac{M{r}^2}{2}$ $I_x=I_y=\frac{M{r}^2}{4}$
Guscio cilindrico di raggio r e massa M.		$I=M{r}^2$
Cilindro di raggio r, altezza h e massa M.		$I_z=\frac{M{r}^2}{2}$   $I_x=I_y=\frac{1}{12}M(3r^2+h^2)$
Tubo di raggio interno r1, esterno radius r2, lunghezza h e massa M.		$I_z=\frac{1}{2}M(r_1^2+r_2^2)=M{r}_2^2(1-t+\frac{1}{2}{t}^2)$   dove t = (r2–r1)/r2 è il rapporto normalizzato dei raggi; $I_x=I_y=\frac{1}{12}M[3({r_2}^2+{r_1}^2)+h^2]$
Tetraedo di spigolo s e massa M.		$I_{solid}=\frac{M{s}^2}{20}$ $I_{hollow}=\frac{M{s}^2}{12}$
Ottaedro (vuoto) di spigolo s e massa M.		$I_z=I_x=I_y=\frac{5M{s}^2}{9}$
Ottaedro (pieno) di spigolo s e massa M		$I_z=I_x=I_y=\frac{M{s}^2}{5}$
Guscio sferico sottile di raggio r e massa M.		$I=\frac{2M{r}^2}{3}$
Sfera piena di raggio r e massa M..		$I=\frac{2M{r}^2}{5}$
Guscio sferico di raggio esterno r2, interno r2 e massa M.		$I=\frac{2M}{5}\left[\frac{{r_2}^5-{r_1}^5}{{r_2}^3-{r_1}^3}\right]$
Cono retto con raggio r, altezza h e massa M.		$I_z=\frac{3}{10}M{r}^2$   $I_x=I_y=\frac{3}{5}M(\frac{r^2}{4}+h^2)$
Toro di raggio a, raggio della sezione b e massa M.		$\frac{1}{8}(4a^2+5b^2)M$
Ellissoide di semiassi a, b, e c con massa M.		$I_a=\frac{M(b^2+c^2)}{5}$ $I_b=\frac{M(a^2+c^2)}{5}$ $I_c=\frac{M(a^2+b^2)}{5}$
Una sottile piatto lastra di altezza h, larghezza w e massa M.		$I_c=\frac{M(h^2+w^2)}{12}$
Parallelepipedo di altezza h, larghezza w, spessore d, e massa M.		$I_h=\frac{1}{12}M(w^2+d^2)$ $I_w=\frac{1}{12}M(h^2+d^2)$ $I_d=\frac{1}{12}M(h^2+w^2)$
Parallelepipedo di altezza D, larghezza W, lunghezza L, e massa M con la diagonale maggiore come asse.		$I=\frac{M(W^2{D}^2+L^2{D}^2+L^2{W}^2)}{6(L^2+W^2+D^2)}$

Raggio giratore

Il momento di inerzia ha le dimensioni di una massa per una lunghezza al quadrato, viene introdotta una lunghezza caratteristica chiamata raggio giratore $r_g$ definito come quella lunghezza al quadrato che moltiplicato per la massa del corpo eguaglia il momento di inerzia cioè:

$I=M{r}_g^2$

di conseguenza:

$r_g=\sqrt{\frac{I}{M}}$

Solo nel caso dell'anello o del guscio cilindrico il raggio giratore coincide con il raggio, negli altri casi il raggio giratore è più piccolo della maggiore dimensione.

Teorema di Huygens-Steiner

Il momento di inerzia di un corpo attorno ad un asse calcolato a partire da quello di un asse passante per il centro di massa e ad esso parallelo.

Quando l'asse di rotazione non passa dal centro di massa del corpo il calcolo del momento d'inerzia potrebbe essere complicato in quanto vengono meno le condizioni di simmetria. Ci viene in aiuto il teorema di Huygens-Steiner che ci dice che il momento d'inerzia di un corpo rispetto ad un asse parallelo che si trova ad una distanza $d$ dal centro di massa è dato da:

$I=I_c+M{d}^2$

Dove $I_c$ è il momento di inerzia di un asse parallelo al primo ma passante per il centro di massa.

La dimostrazione viene fatta assumendo, senza perdita di generalità, che l'origine sia nel centro di massa in un sistema di coordinate cartesiane e che l'asse delle x sia sulla congiungente i due assi. In maniera che il momento di inerzia rispetto all'asse passante per il centro di massa sia:

$I_c=\int (x^2+y^2)dm.$

Mentre il momento di inerzia relativo all'asse z', che è perpendicolare alla distanza d lungo l'asse x dal centro di massa, è:

$I=\int [(x-d{)}^2+y^2]dm$

Sviluppando i vari termini:

$I=\int (x^2+y^2)dm+d^2\int dm-2d\int xdm.$

Il primo termine è $I_c$, il secondo termine è $M{d}^2$ e l'ultimo termine è nullo in quanto l'origine coincide con il centro di massa (l'integrale è pari alla posizione del centro di massa per la massa totale). Quindi, l'equazione diventa come si voleva dimostrare:

$I=I_c+M{d}^2$

(9)

Il teorema di Huygens-Steiner è utile per determinare il momento di inerzia di sistemi complessi come l'esempio di due sfere unite.

Momento angolare nel caso generale

Ritorniamo all'espressione generale del momento angolare:

$\overrightarrow{L}=\int \overrightarrow{r}\times \overrightarrow{v}dm$

Senza perdere di generalità si assume che l'asse attorno a cui avviene la rotazione sia parallelo all'asse $z$ del sistema cartesiano di riferimento. Il momento può essere scomposto in una parte parallela all'asse di rotazione che vale per ogni tratto infinitesimo:

$(\overrightarrow{r}\times \overrightarrow{v}{)}_{z}dm=r^{2}dm\omega$

e quindi, la componente del momento angolare lungo l'asse di rotazione vale:

$L_z=I\omega$

Viene normalmente chiamato momento angolare assiale. Questa componente del momento angolare è indipendente dalla posizione del polo sull'asse di rotazione. Vi è in genere una altra componente ortogonale all'asse di rotazione $L_{\mathrm{\perp }}$ che dipende dalla posizione del polo sull'asse e si annulla se l'asse di rotazione passa per il centro di massa ed è un asse di simmetria. La componente trasversa se presente ruota intorno all'asse di rotazione e può anche cambiare di ampiezza. A causa di questa componente in generale il momento angolare di un solido non è parallelo all'asse di rotazione quindi possiamo scomporre il momento angolare:

$\overrightarrow{L}=L_z+L_{\mathrm{\perp }}$

(11)

Il momento angolare assiale, essendo proporzionale al momento di inerzia del corpo rispetto all'asse per cui viene calcolato, dipende solo dalla forma del corpo e della posizione dell'asse rispetto al corpo.

Assi di simmetria di un corpo rigido

La precessione di una trottola

Se l'asse attorno a cui avviene la rotazione rappresenta un asse di simmetria, cioè le masse sono disposte in maniera simmetrica attorno a tale asse, la componente ortogonale del momento angolare è nulla. Tra gli infiniti assi di rotazione di un corpo rigido passanti per il centro di massa hanno particolare importanza i cosiddetti assi principali di inerzia. Gli assi principali di inerzia sono almeno tre, ma possono essere in numero superiore se il corpo è dotato di particolari simmetrie. Ad esempio nel caso di simmetria sferica qualsiasi diametro è un asse di simmetria. Nel caso di un cilindro l'asse del cilindro è un asse principale di inerzia assieme a qualsiasi asse ad esso perpendicolare. Una rotazione attorno ad un asse principale di inerzia gode della proprietà che il momento angolare del corpo rigido è parallelo all'asse di rotazione e quindi non vi sono sollecitazioni sull'asse di rotazione.

La costruzione di Poinsot permette di ricavare dai momenti di inerzia attorno agli principali di inerzia detti momenti principali di inerzia i momenti di inerzia per qualsiasi asse attraverso la costruzione del cosiddetto ellissoide di inerzia.

L'operazione di equilibratura, che viene fatta sulle ruote delle automobili, consiste proprio nel rendere simmetrico l'asse attorno a cui avviene la rotazione un asse di simmetria, impedendo che sull'asse di rotazione, detto tecnicamente (mozzo), agiscano momenti usuranti. Infatti il fatto che negli elementi ruotanti l'asse di rotazione non coincida con l'asse di simmetria è sempre un qualcosa da evitare per evitare l'usura sui supporti dell'asse di rotazione.

Se la componente normale all'asse di rotazione non è nulla, il moto rotatorio è sicuramente più complesso da studiare ed assume ad esempio la forma di un moto precessione: il tipico moto di una trottola. Nell'esempio in figura l'asse verticale è quello di rotazione, ma il momento angolare ha una componente lungo la direzione verticale ed una nella direzione ad essa perpendicolare che ruota attorno all'asse verticale. Il moto di precessione si ha anche in assenza di una coppia applicata al corpo. In una precessione senza coppia, come nel caso del moto di una trottola lasciata libera, il momento angolare per la seconda equazione cardinale è costante, ma le velocità angolare cambia di orientazione nel tempo. Se cambiano gli assi attorno a cui avviene la rotazione che sono combinazioni quadratiche degli assi principali di inerzia, il momento di inerzia rispetto ad ogni direzione delle coordinate cambia nel tempo, pur conservandosi costante nel tempo. Il risultato è che la componente della velocità angolare del corpo attorno ad ogni asse variererà inversamente con il momento di inerzia rispetto a quell'asse.

Energia cinetica e lavoro

L'energia cinetica del corpo rigido si ricava per estensione di quella di un sistema di particelle:

$E_k=\frac{1}{2}\int v^{2}dm$

Se il corpo è in rotazione attorno ad un asse fisso essendo $v=\omega r$ si ha che;

$E_k=\frac{1}{2}\int {\omega }^2{r}^{2}dm=\frac{1}{2}I{\omega }^2$

Dove $I$ è il momento di inerzia attorno all'asse di rotazione. Se però l'asse di rotazione del corpo di massa $M$ è a distanza $d$ dal centro di massa dal teorema di Huygens-Steiner si ha che:

$E_k=\frac{1}{2}(I_c+M{d}^2){\omega }^2=\frac{1}{2}{I}_c{\omega }^2+\frac{1}{2}M{\omega }^2{d}^2$

ma $\omega d$ è la velocità del centro di massa $v_{CM}$:

$E_k=\frac{1}{2}{I}_c{\omega }^2+\frac{1}{2}M{v}_{CM}^2$

(11)

L'espressione appena data vale anche nel caso più generale del moto rototraslatorio. In cui si ha sia $v_{CM}\ne 0$ che una rotazione attorno ad un asse istantaneo di rotazione. L'espressione separa l'energia cinetica in energia cinetica rotazionale e in energia cinetica dovuta al moto traslazionale del centro di massa.

Abbiamo visto nella dinamica del punto che vi è un legame tra la variazione della energia cinetica ed il lavoro:

$dW=d{E}_k$

Quindi si ha che per quanto riguarda la parte rotazionale dell'energia cinetica:

$dW=d\left(\frac{1}{2}{I}_z{\omega }^2\right)=I_z\omega d\omega =I_z\frac{d\theta }{dt}\alpha dt=I_z\alpha d\theta ={\tau }_{z}d\theta$

Dove $\overrightarrow{\tau }$ è il momento delle forze esterne applicate al corpo rigido. Quindi il lavoro della componente del momento lungo l'asse di rotazione necessario per ruotare il corpo rigido, da un angolo ${\theta }_1$ ad un angolo ${\theta }_2$, vale:

$W=\underset{{\theta }_1}{\overset{{\theta }_2}{\int }}{\tau }_{z}d\theta =\frac{1}{2}{I}_z{\omega }_2^2-\frac{1}{2}{I}_z{\omega }_1^2$

Notiamo che se le forze sono conservative il lavoro può esprimersi come variazione della energia della energia potenziale:

$W=-\mathrm{\Delta }{E}_p$

L'energia totale, e qui teniamo conto anche dell'energia traslazionale del sistema, rimane costante cioè:

$\frac{1}{2}M{v}_{CM}^2+\frac{1}{2}I{\omega }^2+E_p=costante$

Moto di puro rotolamento

Esempio di moto di puro rotolamento di una ruota. Il punto O di contatto istantaneo ha velocità nulla.

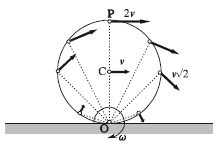
In fisica classica il moto di puro rotolamento è quello in cui un corpo rigido rotola su una superficie ma la velocità istantanea del punto di contatto è nulla. Il corpo ruota così attorno al punto di contatto (che rimane fermo) con il piano. La ruota che ha avuto una importanza fondamentale nello sviluppo della società moderna in condizioni normali di lavoro è ben descritta da questo tipo di moto. La forza di attrito statico è quella che garantisce l'immobilità del punto di contatto, notiamo che dopo un tempo $dt$ il punto di contatto diventa un punto infinitesimo vicino e via di seguito.

La sezione del corpo rigido deve essere un cerchio di raggio $R$ (cioè può essere una ruota, un cilindro, una sfera eccetera).

Indichiamo con $\overrightarrow{R}$ il vettore che ha origine nel centro di massa del corpo rigido C e l'altro estremo sul punto istantaneo di contatto O con il piano di appoggio. La velocità angolare $\overrightarrow{\omega }$ è un vettore normale al piano contenente la sezione del cerchio, con origine nel centro di massa. Nel moto dei corpi rigidi è sempre possibile descrivere il moto di una qualsiasi punto come la combinazione del moto traslatorio del centro di massa e la rotazione attorno ad un asse passante per il centro di massa. In particolare quindi la velocità del punto di contatto è descritta dalla relazione:

${\overrightarrow{v}}_O={\overrightarrow{v}}_C+\overrightarrow{\omega }\times \overrightarrow{R}$

Imponendo che tale velocità sia nulla si ha che:

${\overrightarrow{v}}_C=-\overrightarrow{\omega }\times \overrightarrow{R}$

Quindi se il corpo si muove verso destra, come nella figura, la rotazione avviene in senso orario. In modulo quindi

$v_C=\omega R$

cioè nel moto di puro rotolamento esiste una relazione ben precisa tra la velocità del centro di massa e la velocità angolare (che non dipende dalla scelta del polo). Se quindi la velocità del centro di massa cambia nel tempo, cioè il moto è accelerato, la stessa cosa deve fare la velocità angolare per cui anche:

$|a_{CM}|=|\alpha |R$

avendo indicato con $a_{CM}$ la accelerazione del centro di massa e con $\alpha$ la accelerazione angolare Vale la pena di studiare alcuni casi particolari:

Una ruota soggetta all'azione di una forza F applicata sul centro di massa.

Immaginiamo di avere un corpo rigido a sezione circolare di raggio $R$ e massa $M$ come mostrato in figura su cui agisce una forza motrice sul centro di massa parallela al piano di appoggio orizzontale (questo è il caso delle ruote non motrici di una automobile). La figura mette in evidenza le varie forze agenti sul corpo: la $F$ parallela al piano applicata sul centro di massa; $f$ la forza di attrito statico; la forza peso $Mg$, la reazione vincolare $N$. La reazione vincolare bilancia esattamente la forza peso (se la superficie fosse un piano inclinato l'equazioni sarebbero diverse):

$N=Mg$

Mentre per quanto riguarda la direzione orizzontale, l'equazione oraria ( prima equazione cardinale) è:

$F-f=M{a}_{CM}\to a_{CM}=\frac{F-f}{M}$

Per quanto riguarda il momento angolare ( seconda equazione cardinale), definendo con $I$ il momento di inerzia rispetto all'asse di rotazione del corpo e scelto il centro di massa come polo:

$Rf=I\alpha \to \alpha R=\frac{R^{2}f}{I}$

Eguagliando le due espressioni cioè imponendo che il moto sia di puro rotolamento:

$\frac{F-f}{M}=\frac{R^{2}f}{I}$

L'unica incognita diventa la forza di attrito $f$ che vale:

$f=\frac{F}{1+M{R}^2/I}$

Quindi la forza di attrito in modulo è sempre inferiore al valore della forza trainante. Ma in ogni caso deve anche valere la condizione che:

$f\le {\mu }_{s}N={\mu }_{s}Mg$

Questo impone che per garantire un moto di puro rotolamento la forza da applicare al centro di massa deve essere inferiore ad un certo valore massimo:

$F_{max}\le {\mu }_{s}Mg(1+M{R}^2/I)$

Notare che se venisse applicata una forza maggiore di $F_{max}$, il punto di contatto striscerebbe, in quanto la forza di attrito statico non sarebbe più sufficiente a bloccarlo sul piano di appoggio, si avrebbe quindi che il moto non sarebbe di puro rotolameneto in quanto:

$|{\overrightarrow{v}}_C|>|\overrightarrow{\omega }\times \overrightarrow{R}|$

Via via che crescesse la forza applicata il moto traslatorio prevalerebbe sul moto rotatorio.

La funzione dell'attrito statico è essenziale nel moto di puro rotolamento, in quanto causa un momento di una forza (fR) che fa ruotare il corpo, e quindi il corpo trasla (per effetto della forza F applicata) e contemporaneamente ruota a causa dell'attrito. Se non ci fosse attrito il corpo semplicemente traslerebbe. Notare che se la sezione del corpo ruotante non è perfettamente circolare il moto diventerebbe in quei punti di contatto prevalentemente traslatorio e la forza di attrito svolgerebbe anche un'azione frenante; l'esempio più chiaro è il caso delle ruote delle automobili non motrici sgonfie.

Se la forza fosse stata frenante, quindi con direzione opposta alla direzione del moto, anche la forza di attrito avrebbe avuto direzione opposta, matematicamente tutte le equazioni sarebbero rimaste eguali, $F_{max}$ sarebbe la forza frenante massima applicabile.

Moto di puro rotolamento con solo momento applicato sull'asse

Ruota di massa m (nel testo M) soggetta ad un momento $\tau$ applicato all'asse di rotazione.

Immaginamo di avere una ruota sul cui asse è applicato un momento motore $\tau$. Questo è il caso delle ruote motrici di una automobile. Nella figura sono mostrate le forze ed il momento. Immaginiamo che il moto si svolga su un piano orizzontale. Notare che il verso della forza di attrito è opposto al caso precedente.

La reazione vincolare bilancia esattamente la forza peso come nel caso precedente. Ma per quanto riguarda la componente orizzontale si ha:

$f=M{a}_{CM}\to a_{CM}=\frac{f}{M}$

Per quanto riguarda il momento angolare, tenendo presente che se il momento fa ruotare il corpo in senso orario, la forza di attrito esercita un momento in direzione opposta:

$\tau -Rf=I\alpha \to \alpha R=\frac{\tau R-R^{2}f}{I}$

Eguagliando le due espressioni (condizione necessaria per avere moto di puro rotolamento):

$\frac{f}{M}=\frac{\tau R-R^{2}f}{I}$

Da cui si ricava che $f$ vale:

$f=\frac{\tau }{R(1+I/M{R}^2)}$

la forza d'attrito è la forza motrice che causa il moto traslatorio, ma anche in questo caso si ha la condizione che:

$f\le {\mu }_{s}N={\mu }_{s}Mg$

e quindi:

${\tau }_{max}\le {\mu }_{s}MgR(1+I/M{R}^2)$

Se il momento applicato è maggiore di ${\tau }_{max}$ il moto rotatorio è prevalente sul moto traslatorio. Questo è il caso delle ruote motrici di una automobile quando su di esse viene applicato un momento maggiore di quello che permette la trazione e le ruote slittano. La forza di attrito è la forza che causa il moto traslatorio, la ragione per cui gli pneumatici delle automobili sono fatti di gomma è per avere un elevato attrito statico con il fondo stradale.

Notiamo che se ci fosse stato un momento frenante la forza di attrito avrebbe avuto verso opposto, ed avrebbe quindi l'effetto di rallentare il moto. Ma l'espressione del momento massimo applicabile sarebbe stata la stessa.

Moto di puro rotolamento con un momento ed un forza applicata

Ruota di massa m (nel testo M) che sale su un piano inclinato spinta da un momento $\tau$ che agisce sul suo asse.

Immaginiamo che il moto si svolga su un piano inclinato in salita con inclinazione $\theta$, sul corpo agisce un momento motore $\tau$. La forza peso ha una componente tangenziale al piano $Mg\sin \theta$ e una normale $Mg\cos \theta$. La reazione vincolare bilancia esattamente la componente della forza peso perpendicolare al piano:

$N=Mg\cos \theta$

Mentre la legge del moto nella direzione del piano di appoggio è:

$M{a}_{CM}=f-Mg\sin \theta \to a_{CM}=\frac{f}{M}-g\sin \theta$

Per quanto riguarda il momento angolare tenendo presente che, se il momento fa ruotare il corpo in senso orario, la forza di attrito esercita un momento in direzione opposta:

$\tau -Rf=I\alpha \to \alpha R=\frac{\tau R-R^{2}f}{I}$

Dalla condizione che il moto sia di puro rotolamento segue che:

$f=\frac{\tau /(R)+Ig\sin \theta /(R^2)}{1+I/(M{R}^2)}$

Imponendo la condizione che:

$f\le {\mu }_{s}N={\mu }_{s}Mg\cos \theta$

Si ha che per avere moto di puro rotolamento:

${\tau }_{max}\le {\mu }_{s}MgR\cos \theta (1+I/M{R}^2)-\frac{Ig}{R}\sin \theta$

Vi è anche una inclinazione massima del piano inclinato al di sopra della quale qualsiasi moto di puro rotolamento non è possibile (quando è nullo ${\tau }_{max}$) cioè se si ha che $\theta \ge arctg\left[{\mu }_s(M{R}^2/I+1)\right]$.

In discesa $\theta <0$ è possibile un moto di puro rotolamento anche in assenza di attrito per un opportuno momento motore. Se in discesa $\tau /(MR)<-Ig\sin \theta /(R^2)$ la forza di attrito cambia segno rispetto a quanto indicato nella figura.

Attrito volvente

Nel moto di puro rotolamento la forza di attrito statico non esercita nessun lavoro in quanto il punto di applicazione non cambia. Bisogna aggiungere che pure nei corpi che rotolano senza strisciare si nota che si fermano dopo un certo tempo o se si vuole un piano inclinato inferiore ad una certa pendenza non riesce a fare rotolare oggetti di sezione circolare. La giustificazione che viene data è che esiste un attrito dovuto alla deformazione locale del piano di appoggio (il corpo rigido è indeformabile per definizione, ma nella pratica è deformabile anche esso). Il coefficiente di attrito volvente produce un momento frenante pari a :

${\tau }_f=hN$

con $h$ coefficiente di attrito volvente, che ha le dimensioni di una lunghezza (la massima deformazione), $N$ la reazione vincolare. In genere l'attrito volvente esercita una azione trascurabile. Ma sicuramente una automobile con gli pneumatici sgonfi si arresta molto prima, una volta spento il motore.

Esempio di attrito volvente.

Pendolo composto

Un pendolo composto

Chiamiamo pendolo composto o fisico un corpo rigido che oscilla attorno ad un asse orizzontale non passante per il centro di massa.

Spostando il pendolo composto dalla posizione di equilibrio di un angolo $\theta$, il momento della forza peso tende a riportare il pendolo verso la posizione di equilibrio. Il momento della forza peso, che agisce come un momento di richiamo verso la posizione di equilibrio, è parallelo all'asse di rotazione e vale

$M=-MgL\sin \theta$

dove $L$ è la distanza tra il centro di rotazione ed il centro di massa (non è il momento angolare). Supponendo trascurabile l'attrito nella rotazione attorno all'asse e supponendo che eventuali momenti dovuti alle reazioni dei supporti risultano ortogonali all'asse stesso, l'equazione seconda equazione cardinale diventa:

$\frac{d{L}_z}{dt}=I\alpha =I\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}=-MgL\sin \theta$

Indicando con $I$ è il momento di inerzia del corpo rispetto all'asse di rotazione orizzontale z passante per la posizione di equilibrio. Quindi:

$\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}+\frac{MgL\sin \theta }{I}=0$

Se l'ampiezza delle oscillazioni è piccola, usando lo sviluppo di Taylor, si può approssimare $\sin \theta$ con $\theta$, ottenendo

$\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}+\frac{MgL\theta }{I_z}=0$

che è l'equazione del moto armonico la cui equazione oraria è:

$\theta ={\theta }_0\sin (\mathrm{\Omega }t+{\phi }_0)$

La pulsazione è

$\mathrm{\Omega }=\sqrt{\frac{MgL}{I_z}}$

e il periodo vale

$T=\frac{2\pi }{\mathrm{\Omega }}=2\pi \sqrt{\frac{I_z}{MgL}}=2\pi \sqrt{\frac{l}{g}}$

dove $l=I_z/ML$ rappresenta la lunghezza ridotta del pendolo composto e corrisponde alla lunghezza del filo di un pendolo semplice che oscilla con lo stesso periodo.

Quando l'ampiezza delle oscillazioni è grande il pendolo si muove ancora di moto periodico, ma non più armonico.

Esempio sul pendolo fisico.

Impulso angolare

Nel caso di un momento applicato $\overrightarrow{\tau }$ ad un corpo rigido che agisce per un limitato intervallo $\mathrm{\Delta }t$ di tempo la grandezza:

${\overrightarrow{J}}_{\tau }=\overrightarrow{\tau }\mathrm{\Delta }t$

viene chiamata impulso angolare. La sua azione su un corpo rigido e quella provocare una variazione del momento angolare, cioè:

${\overrightarrow{J}}_{\tau }=\mathrm{\Delta }\overrightarrow{L}$

cioè la sua azione è simile a quello che avviene per la variazione della quantità di moto per forze impulsive. Anche in questo caso se la durata del momento impulsivo è breve, tutte gli altri momenti agenti possono trascurarsi.

Esempio:
Immaginiamo di avere una sbarretta di lunghezza $\ell =42cm$ e massa $M=2.05kg$ incernierata ad un 
estremo ad un perno fisso orizzontale che può muoversi liberamente in un piano verticale se viene
applicato un impulso angolare di ${\overrightarrow{J}}_{\tau }=1kgms$ poiché il suo momento di inerzia rispetto ad un
estremo è $I_c=M\ell /3=0.12kg{m}^2$ acquisterà una velocità angolare: $\omega =J_{\tau }/I_c=8.3rad/s$ e
quindi una energia cinetica rotazionale di $E_k=\frac{1}{2}{I}_c{\omega }^2=4.15J$ che diventa energia  potenziale
nel punto più alto $E_p=Mgh=E_k$, cioè $h=E_k/(Mg)=0.21m$ (cioè compie un quarto di giro)

Statica

La condizione necessaria affinché un corpo rigido sia in equilibrio statico è che contemporaneamente:

$\overrightarrow{R}=0$

$\overrightarrow{\tau }=0$

e che né si muova il centro di massa e né ruoti attorno a qualsiasi polo

Alcuni esempi chiariscono meglio la statica dei corpi rigidi: scala con una persona, asta orizzontale con un carico.

Bibliografia

• Template:Cita libro

Altri progetti

 Argomento seguente: Urti